Computer architecture
Introduction
In this chapter we will look at the architecture, or fundamental structure, of modern computers. In the previous chapters we examined the theoretical underpinnings of why computers work. By the end of this chapter, you will have a much better understanding of how computers work.
We will begin by studying the micro-architecture of computing components. That covers the very low level, fundamental questions of how information can be physically encoded and computed by a digital circuit. We’ll look at binary and hexadecimal number systems and study how computational instructions are encoded. We will study logic gates, the basic building blocks of digital circuits, to understand how computational and storage units are constructed. Having covered that, we’ll expand our focus to the overall computer architecture. To understand exactly how computation happens, we’ll dive into the internal architecture and operation of the processor. We will also look at the other essential component, memory, and how it is arranged into a hierarchy of caches.
Modern computing components, in particular processors, are incredibly sophisticated. We’ll mostly focus on a very simplified architecture so that you can understand the overall design without getting too bogged down in various implementation details. Nevertheless, we’ll round off the chapter with a discussion of some sophisticated optimisations found in real world systems.
At various points in the chapter we’ll use the example of a simple addition instruction to illustrate what’s going on.
Representing information
The definition of a Turing machine is a bit vague about how information should be provided to the machine. It just states that “symbols” are written on the input tape. Which symbols should we use? Over the years, computer designers experimented with a number of approaches but settled fairly quickly, for reasons we’ll see, on binary encoding. Let’s look at what that means.
Number bases
A single binary value is known as a bit. It can only be one of two values: 0 or 1. The equivalent in the decimal system is a digit, which can be one of ten values: 0-9. Having only two possible values doesn’t seem all that great. How might we express a value greater than 2 in binary? Well, when we want to express a value bigger than 9 in decimal, we just add more digits. Each new digit allows ten times more numbers:
| 100s | 10s | 1s | number of possible values |
|---|---|---|---|
| 9 | 10 | ||
| 9 | 9 | 100 | |
| 9 | 9 | 9 | 1000 |
You might remember learning in school that the rightmost column in a number is the units, the next one to the left is the tens, the next the hundreds and so on. In general, n columns can express 10n values. The principle is exactly the same in binary, except we use 2n:
| 8s | 4s | 2s | 1s | number of possible values |
|---|---|---|---|---|
| 1 | 2 | |||
| 1 | 1 | 4 | ||
| 1 | 1 | 1 | 8 | |
| 1 | 1 | 1 | 1 | 16 |
The value of n is known as the base of the counting system. Decimal uses 10 as its base. Binary uses 2.
Try writing out every combination of three bits (000, 001, 010 and so on). You will find that there are eight. Adding an extra bit doubles the number of possible values. So adding more bits allows for a greater range of values. The computing industry has managed to agree that eight bits, known as a byte, are the minimum value size. Bytes form the basic building block of every value and data type.
Why eight and not seven or nine? It’s mostly a convention, though there are some advantages to eight bits. As we’ll see shortly, components capable of handling large values are frequently constructed by combining a pair of smaller components. Each pairing doubles the value size, meaning that values that are a power of two, such as 8 (23), are a more natural fit.
Bytes can be written bit by individual bit. Here is 255: 0b11111111. Binary numbers are conventionally written with a leading 0b, indicating that 0b11 represents binary three and not decimal eleven. However, for humans it’s slow and difficult to read long sequences of 1s and 0s. Is 0b1111111111111111 the same as 0b111111111111111? It’s difficult to tell without counting each bit.
Hexadecimal is an alternative number system that uses sixteen as its base. It uses the standard 0-9 for the first ten values and then A-F to express the remaining six (10-15 in decimal). Hexadecimal values are conventionally prefixed with 0x to make clear that we’re working with hexadecimal.
| 4,096s | 256s | 16s | 1s | number of possible values |
|---|---|---|---|---|
| F | 16 | |||
| F | F | 256 | ||
| F | F | F | 4,096 | |
| F | F | F | F | 65,536 |
Looking at the tables above, we see that four bits (0b1111) can hold the same number of values as a single hexadecimal value (0xF). This means that a byte can be expressed as two hexadecimal values, which is much easier to read. Here is how we convert from binary to hexadecimal:
1. Take a byte value e.g. 0b10110011 and split into halves: 0b1011 0b0011
2. Convert each half to decimal: 11 3
3. Convert each half to hexadecimal: 0xB 0x3
4. Squish halves together: 0xB3
It’s important to see that expressing a binary number in hexadecimal doesn’t change its value. It’s just a different way of expressing the same thing. 0x54 is not the same as decimal 54. Can you work out what it is in decimal? We have four ones and then five sixteens, so it is 5 * 16 + 4 * 1 or 84 in decimal.
As a web developer, your main exposure to hexadecimal is almost certainly going to be CSS colour values, which are RGB (red, green, blue) colours encoded in hexadecimal. The RGB format has one byte encoding the amount of red, one for the amount of green and one for the amount of blue. White is therefore full red, full green and full blue: 0xFF FF FF. Black is no red, no green and no blue: 0x00 00 00. Armed with this understanding of hexadecimal, you can impress your friends and colleagues by editing colour values directly! You might have a grey like 0xADADAD but think that it looks a little dark. You can brighten it by increasing the value for each component by the same amount: 0xDEDEDE. Hours of fun!
According to how I’ve written the binary numbers, as you move from right to left, each column represents a value double the size of the previous one. This matches how we write decimal numbers, where the most significant digit comes first: in 123 the 1 represents hundreds and the 2 represents tens. The 1 is more significant because the number it represents (100) is bigger than the number the 2 represents (20). This is just a convention. Everyone could decide tomorrow to do things in reverse and write 123 as 321 and everything would be fine as everyone followed the same convention. Sadly, the computing industry hasn’t quite reached the same level of cohesion on how to order the bytes in binary numbers. In a binary number made up of multiple bytes, one will be the most significant byte (MSB) and another will be the least significant byte (LSB). In the number 0x5566, 0x55 is most significant because it represents 0x5500, which is bigger than 0x0066. In a system using big endian ordering, that number would be represented with the following two bytes: [0x55, 0x66]. In a little endian system it will be represented the other way around: [0x66, 0x55] Nowadays the majority of processors are little endian but network protocols are big endian, just to keep people on their toes.
Negative numbers
We’ve seen that a byte can express a value between 0 and 255. We can encode bigger numbers by sticking bytes together. Two bytes is sixteen bits and so can encode 216 (65,536) values. We can always express a bigger positive integer by adding more bytes. How can we go in the other direction and express a negative number? All we need is an agreed way to encode them. The most common encoding is known as two’s complement.
To encode a negative number in two’s complement, just take the positive number, flip all the bits and add one. So to encode -2:
1. Encode +2 in binary: 0b00000010
2. Flip each bit: 0b11111101
3. Add one: 0b11111110
The reason for using this particular encoding is that negative and positive numbers can be added, subtracted and multiplied together as normal without any special handling. Look at what happens when we add 1 to -2 three times. Things just work out properly:
1 0b11111110 + 0b00000001 = 0b11111111 // -1
2 0b11111111 + 0b00000001 = 0b00000000 // 0
3 0b00000000 + 0b00000001 = 0b00000001 // 1
There are two interesting things to note. Firstly, this is where the distinction between signed and unsigned integers comes from. An unsigned integer holds only positive numbers. A signed integer uses two’s complement to encode both positive and negative numbers. This means it can’t hold as many positive numbers because half of the possible bit patterns are for negative numbers. For example, an unsigned byte can hold 0 to 255 and a signed byte can hold -128 to 127.
Secondly, observe that there is nothing inherent in 0b11111110 that makes it a negative number. It all depends on how we instruct the computer to interpret it. If we say it’s an unsigned byte, the computer will interpret it as 254. If we say it’s a signed byte, it will interpret it as -2. Everything is just a series of bits to the computer. It is the programmer who imposes meaning by instructing the computer how to interpret them.
Decimal numbers
All of the above applies only to whole numbers. Decimal numbers, such as 1.222, are encoded in a representation known as floating point. The value is stored as a significand scaled by an exponent. 1.222 would be represented as 1222 * 10-3. The name comes from the fact that the decimal point moves around depending on the exponent’s value.
The exact details of how values are encoded will vary with the processor’s floating point implementation, but they all suffer from the same problem of imprecision. Between any two decimal values there is an infinite number of other decimals. It’s not at all obvious how the finite number of bit patterns should map to these infinite values.
In order to encode a value into a fixed number of bits (normally 32 or 64), the significand must be approximated to a fixed number of bits. For example, imagine that a decimal floating point encoding only allowed four digits for the significand. 1.2223 and 1.2219 would be rounded down and up respectively to 1222 * 10-3. Floating point values are therefore imprecise. The deviation compounds when you perform arithmetic and this can lead to confusing results. In my Firefox browser, 3.0 * 2.02 does not equal 6.06, as you would expect, but 6.0600000000000005. Whenever you perform calculations that need to be exact, such as when dealing with money, it is better to convert the values to whole numbers (e.g. convert dollars to cents), perform the calculation and then reverse the scaling.
Instruction sets
Recall the Turing machine. It reads a series of symbols from the input tape. Each symbol causes the finite state control to respond in a certain way. We can therefore think of the symbols as instructions to the Turing machine. To implement instructions for a real computer, we must first answer two questions: what instructions do we have and how should we encode them in binary? Let’s use the example of an instruction to add two numbers together. We now know that the two values can be stored in binary-encoded bytes. Since the computer only understands binary, the instruction must also be in a binary form. Binary-encoded instructions are known as machine code.
Each processor accepts an instruction set of valid, binary-encoded instructions. The architecture of the processor – its internal components and how they are wired together – determines its capabilities and so defines the set of valid instruction and how they are encoded in binary. Naturally, it wouldn’t make sense for the instruction set to include an instruction which the processor lacked the circuitry to execute. The problem then is that every processor design would have a different architecture and so a completely different instruction set. Writing portable code would be exceptionally difficult.
The instruction set architecture (ISA) provides the missing layer of abstraction. It’s an abstract model of the processor’s architecture that separates the external, programmer-facing interface from the internal implementation details. Processors can have different internal architectures but still implement the same ISA, meaning that they are binary compatible: machine code for one processor will run on the other without modification.
Certain ISAs have become dominant within the computer industry. Since code written for one ISA is not compatible with other ISAs, if you’re an upstart processor manufacturer it makes sense to design a processor that implements the incumbent’s ISA. Your processor will be more attractive if it can run existing code without modification and you can still compete on cost or implementation performance. This is exactly what AMD did when they took on Intel. Intel’s x86 instruction set was so dominant that AMD had to make sure their processors implemented the x86 interface, even if they worked very differently internally.
Let’s look at two popular ISAs: x86 and ARM. They are both extremely popular and represent two opposing design philosophies. They are mutually incompatible. x86 code will not run on an ARM processor and vice versa.
Processor manufacturers initially competed by adding more and more complicated instructions to their ISA. The thinking was that a programmer would prefer a processor that offered sophisticated instructions for things such as finding a square root because that would mean less work for the programmer. Rather than having to write and test a square root function, they could just use the built-in instruction. The problem is that more complex instructions require more complex circuitry, making the processor bigger, slower and more expensive. This approach is known as complex instruction set computing (CISC). Intel’s x86 is the classic example of a CISC ISA. It began with Intel’s wildly popular 8086 processor in 1978. That processor’s instruction set is actually relatively straightforward by modern standards, but over the years more and more backwards-compatible extensions were added and what we have now is a bit of a beast. The majority of desktop and laptop computers contain x86 processors.
Another approach is to provide a relatively limited set of simple instructions. If the programmer wants to do anything fancy, they’ll have to implement it themselves out of these building blocks. The benefit of this is that the processor has a less complex design, making it easier to optimise for size, speed and energy consumption. This approach is called reduced instruction set computing (RISC) because the set of available instructions is deliberately reduced compared to what a CISC processor offers. A program written for a RISC processor will have more instructions than one written for a CISC processor. However, with time it’s proven easier to optimise RISC processors and so the RISC processor will be able to churn through those instructions at a faster rate. This is the approach that ARM processors take. Their high efficiency means they are particularly attractive for mobile devices. The majority of phones and tablets use processors that implement the ARM instruction set, making it the most popular ISA overall.
RISC versus CISC was one of those interminable wars that the computer industry loves to wage against itself. As time has passed, the sharp distinction between the two philosophies has blurred somewhat. ARM has picked up various extensions that have added complexity. Intel found the x86 ISA so difficult to optimise that they actually added an extra step (invisible to the programmer) that converts x86 instructions into a RISC-like internal instruction set. It’s these micro-ops that are actually executed by Intel processors. This further demonstrates how ISAs act as an interface. Just as with a programming interface, it’s possible for a processor designer to completely change the interface’s implementation, as long as the externally-facing parts remain constant.
The MIPS ISA
In this section we will study the MIPS ISA to better understand how an ISA is designed. I’m using the MIPS ISA because it’s specifically designed for teaching purposes. It’s comparatively simple but has enough complexity to demonstrate the tricky design challenges.
Very roughly, processor instructions fit into three categories: computation, control flow and memory operations. In MIPS these correspond to R instructions (for “register”), J instructions (for “jump”) and I instructions (for “immediate”). Every MIPS instruction is a sequence of 32 bits. Each instruction format specifies how the bit sequence is divided into fields specifying various locations, operations and so on.
It’s difficult for humans to look at a sequence of 32 bits and determine where one field starts and the other ends. Instructions are therefore usually expressed in assembly language. In assembly, each instruction is given a short mnemonic with arguments corresponding to the instruction’s bit fields. Assembly is not a programming language per se in the same vein as C or JavaScript. Each ISA will have its own, unique assembly language. A program written in one processor’s assembly will not work on another. Translating assembly code into machine code is a relatively straightforward task performed by an assembler. For each of the instructions examined below, I’ve also included their MIPS assembly name.
To achieve our goal of adding two numbers, we need to use an ADD instruction, which is an R-format instruction.
MIPS R instructions:
A register is a special memory location which holds a single, working value. They are located right in the heart of the processor, meaning that they can be accessed extremely quickly but there is only enough space for a few dozen. The processor cannot operate directly on values stored in memory. Whenever it wants to operate on a value, it has to first load that value from system memory into a register. The output of the instruction’s execution is also written into a register, from where another instruction can write it back to memory.
The size of the registers determines the word size, which is the processor’s unit size for data. It is nearly always a multiple of bytes. MIPS has a 32 bit word size so its registers are 32 bits wide.
In MIPS, the R instruction specifies two registers in which the input values are expected to be stored, a destination register and an opcode which specifies the operation to perform. Common operations include addition, multiplication, negation and logical bitwise operations (e.g. AND, OR). MIPS doesn’t provide a subtraction operation because that doesn’t need a dedicated instruction. You can subtract by negating one input and then adding – an example of a reduced instruction set!
| opcode | rs | rt | rd | shift (shamt) | funct |
| 6 bits | 5 bits | 5 bits | 5 bits | 5 bits | 6 bits |
We can see that an R instruction, like all MIPS instructions, is 32 bits long. The first 6 bits specify the opcode. 6 bits means we can have 26, or 64, different operations. Next, we have the three registers. rs and rt are inputs and rd is the destination. 5 bits per register mean we can specify up to 32 different registers. We’ll skip over the shamt as it’s not relevant. Finally, we have 6 bits for the funct. Being able to specify 64 opcodes seems like a lot, but it’s actually fairly limiting. To get around this, some instructions share an opcode but are uniquely identified by the funct at the end. All R instructions share the same 0b000000 opcode. We’ll look at why there’s this split between the opcode and funct fields later.
Here’s how our ADD instruction looks in MIPS assembly:
1 // means a comment
2 ADD $d, $s, $t // $d = $s + $t
And the binary encoding:
1 0000 00ss ssst tttt dddd d000 0010 0000
The processor knows it’s an R instruction because it has 0b000000 at the left. It then knows that the bits in the middle encode the various registers. It can identify that it’s an ADD instruction because the funct field on the right contains 0b100000, which the MIPS ISA defines to be the funct code for addition.
We can create instructions for other R operations just by changing the funct value. For example, 0b100101 is the funct code for bitwise OR, which compares two values bit by bit and writes a 1 to the corresponding destination bit if either of the inputs are 1 and a 0 if not.
MIPS J instructions:
Normally the processor executes instructions one after the other. Sometimes we need the ability to move, or jump, to a different instruction. Perhaps we want to execute a function located elsewhere in memory. J instructions tell the processor to jump to the instruction at a specified address.
The encoding of J instructions is much simpler. Apart from the opcode, the whole instruction is given over to specifying the memory address to jump to. The instruction directly encodes the address:
| opcode | pseudo-address |
| 6 bits | 26 bits |
1 J 0x0003
2 0000 1000 0000 0000 0000 0000 0000 0011
The processor takes the 26-bit pseudo-address, does a little bit of processing to generate the actual address and sets the result as the next instruction to be executed. The processor knows that it has a J instruction because the six bits on the left are 0b000010.
MIPS I instructions:
We are missing two crucial abilities: making decisions and moving values in and out of memory. In MIPS, such instructions are in the I, or immediate, format. They are a hybrid of the previous two. They can specify a number of registers for argument values, just like the R format, but they also contain a offset value encoded directly, or immediately, in the instruction:
| opcode | rt | rs | offset |
| 6 bits | 5 bits | 5 bits | 16 bits |
As mentioned above, a value needs to be loaded into a register before the processor can operate on it. This is handled by the LB (load byte) instruction:
1 LB $t, offset($s) // $t = MEMORY[$s + offset]
2 1000 00ss ssst tttt iiii iiii iiii iiii
Processors often offer a variety of sometimes quite complex ways to compute a memory address. They are all designed to suit a particular use case. Here we expect $s to already contain a memory address. The offset is added to the address and then the value at that location loaded into $t. This may initially appear a convoluted way of doing things. Why not simply specify the address in the instruction? This instruction is useful because we often know that a value will be at a fixed offset to some base element but we don’t know where the base will be located in memory. Can you think of when this situation might occur? Referring back to the chapter on data structures, we iterate through an array by loading the base value into $s and adding offsets encoded directly in the instruction.
When we execute a conditional statement, we perform a branch. BEQ (branch on equal) is a MIPS conditional that compares the values in two registers and if they are equal branches, or jumps, to a specified offset from the current instruction. Otherwise, the subsequent instruction is executed as normal. MIPS also includes BNE (branch on not equal) and instructions to branch if one value is less than another.
1 BEQ $s, $t, offset // if $s == $t then jump by the specified offset else continue
2 0001 00ss ssst tttt iiii iiii iiii iiii
Standard if/else control flow can be encoded in branch instructions by putting the “else” branch directly after the conditional and the “if” branch after the “else” branch. Since we know the size of the “else” branch, we can encode the offset to the “if” code in the instruction. If the condition holds, the processor will jump to that location and execute the “if” branch instructions. If not, it will continue as normal to the “else” branch instructions.
Some ISAs, like x86, have variable-length instructions. In MIPS, each instruction is the same length because that makes the circuitry easier to design. A fixed length means that you have to be clever to make the best use of the space available. This explains why the R instructions have both an opcode and a function specifier. The obvious approach would be to just make the opcode long enough for every instruction to have a unique opcode. The problem is that a longer opcode in every instruction would reduce the number of bits available in the J and C instructions for the memory addresses and offset values. Since function selection is only required for R instructions, it makes more sense to shorten the opcode as much as possible and only include the additional funct field in the R instructions, where it’s actually needed.
Circuits and computation
We now know how data and instructions can be encoded efficiently in a binary format. Why go to all the bother of using binary in the first place?
In theory, there’s nothing preventing us from making a computer that uses ten different voltage levels to encode decimal values. In fact, some early computers did so. The decision to use binary encoding is really just a practical engineering decision. Binary and decimal encodings have the same capabilities – there’s nothing that can be done in binary that can’t be done in decimal, and vice versa – so the decision to use binary is based on what’s physically easier and cheaper to manufacture.
You might remember making simple electrical circuits in school. You hook up a little light bulb to a battery, press a switch and the bulb shines! Such circuits are analogue because the voltage across the circuit has an infinite number of possible values. We could encode bits in an analogue circuit by declaring that one voltage level represents binary 1 and another represents binary 0. Whenever the voltage is at either level, the circuit is outputting the corresponding bit. The problem with an analogue circuit is that there will often be situations where the voltage doesn’t match our specified values. What we really want is a digital circuit in which the voltage can only be one of two possible values. To do this we need components, known as transistors, which can only output two voltage levels. One of the great engineering achievements of the 20th century was the production of very cheap and very small transistors.
Logic gates
Transistors can be combined together to make basic components called gates. A gate receives a number of input voltages and will output the voltage corresponding to either 0 or 1 depending on the inputs it receives. This is how we represent elementary logic in a physical circuit. The internal arrangement of transistors within the gate determines how it responds to input. Circuits using these components implement what is known as combinational logic. There is no concept of state or time within these circuits. Changing the input values immediately leads to a different output.
Some transistor arrangements are particularly useful and have been given names. A NOT gate takes one input and outputs the opposite. An AND gate takes two inputs and outputs 1 if both inputs are 1. An OR gate will output 1 if either of its inputs is 1. A NAND gate does the opposite of an AND gate: it outputs 1 unless both inputs are 1. With these simple components, we can construct circuits implementing arbitrary logical statements simply by arranging gates in the correct order. One of the interesting properties of these gates is that they can all be constructed from just NAND gates. It’s fun to see how this works.
Below is the truth table of a NAND gate. It shows a NAND gate’s output for all possible inputs:
| input A | input B | output |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Below is the truth table for an AND gate:
| input A | input B | output |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
How could you arrange NAND gates so that the circuit implements the AND truth table?
Well, clearly the output of AND is the inverse of NAND. One solution would be to pass our inputs to a NAND gate and then invert the output. How do we perform the inversion? We need to make a NOT gate and then feed the NAND output into the NOT gate. Looking more closely at the NAND truth table, we see that the output of a NAND gate is always the opposite of the input when the input values are the same. To create a NOT gate, all we need to do is send the same voltage to both inputs of a NAND gate!

Using the NOT and AND gates we constructed above, try to work out how you would construct an OR gate implementing the following truth table:
| input A | input B | output |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Simple components
In programming, we reduce complexity by composing larger components out of smaller ones. Ideally, a component will expose a minimal interface to the rest of the application. Anything utilising the component only needs to know the interface and can be blissfully ignorant of the component’s nitty-gritty implementation details. We saw this idea in the distinction between data types and data structures. Digital circuits are no different.
We can package some NAND gates into a particular arrangement and call it an AND gate. Once we’ve verified that this arrangement of NAND gates demonstrates the behaviour specified by the AND truth table, we can treat it simply as an AND gate and ignore its implementation details. Multiple gates can be combined into simple components and then these components can be combined into more complex components. Each stage abstracts away the details of the previous stage, thus keeping the complexity manageable.
One of the simplest components is the half-adder, which adds two binary digits. It has two outputs: the sum and the carry. Just like you need to carry a digit if a sum is greater than 9, you need to carry a bit if the output is greater than 1. The half-adder truth table looks like this:
| input A | input B | sum | carry |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
If you add a 1 and 0 you get 1, as expected. If you add 1 and 1, you get a 0 and a 1 carried over. This is 0b10 or binary two. Can you figure out how to construct a half-adder from NAND gates?
If we chain a series of half-adders together, the output of one feeding into an input of the next and so on, we can create adders capable of adding binary numbers of arbitrary length. This is a huge step up in our capabilities. Two other fundamental components are multiplexers, which take multiple inputs and use a control signal to determine which one to output, and demultiplexers, which take one input and use a control signal to determine which of multiple outputs to send it to. These components can in turn be composed together to make still more complex components.
It’s very tempting to anthropomorphise computers and say things like “it’s thinking” or “it wants me to do something”. What computers can do is so complex that it seems like there must be some kind of intelligence in there. Yet when you dig down into the circuits, you see that computers are nothing more than electrical signals shunting along through lots of very simple components arranged in particular patterns. There is no real decision-making ability in the gates and components. Their design compels them to respond to their inputs in a particular way. There is intelligence in the design of circuits, but it is in the minds of the humans who arranged the components in that particular pattern to achieve those particular outcomes.
Circuits with memory
Combinational logic had no concept of state. The output of the circuit is entirely determined by the current inputs. This poses a problem: how can we store values to use later? It seems that the circuitry we’ve seen so far has no way of building components that can remember things. No combinational logical component will do the job. We need additional concepts.
To be able to use a value “later” implies some kind of time that is different to now. Combinational logic is all about the now. It has no idea what happened before the inputs took their current form. We need a way of dividing time into before and after: a clock. In digital circuits a clock is a component that outputs a signal that alternates rapidly between two values at a regular frequency. Either the rising edge or falling edge can be defined as the start of a new clock cycle.
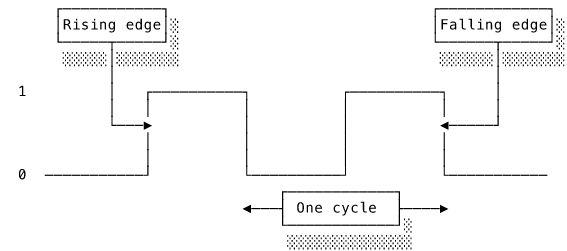
Armed with our ability to measure time, we can now examine some new components. The first is known as a flip-flop. A flip-flop has an input and a control signal. Whenever it receives a control signal, it “latches” on to the input value at that moment and continues outputting that value until another signal tells it to latch on to a new value. It thus “remembers” the input value at the time of the control signal. Each flip-flop can hold one bit. This is our first example of memory within a circuit.
Computer memory is not much more complex than huge banks of flip-flops arranged into bytes, kilobytes, megabytes and so on. Flip-flops require electricity to keep holding on to the value. This is why your computer memory is wiped clean when you power off. Think of how you might temporarily remember a phone number by repeating it to yourself. As soon as you stop repeating it, you forget it.
The clock speed determines the overall performance of the processor. Flip-flops latch on to their input at the beginning of a cycle. This means that we need to have the value we want to store ready by the end of the preceding cycle. It doesn’t matter whether we were ready right at the start of the cycle or only just managed it before the cycle ended. The value won’t be used until the start of the next cycle. A particularly fast bit of circuitry that could perform five calculations within a single clock cycle would be useless because the rest of the system wouldn’t be ready to consume any values until the next clock cycle. The clock speed sets the speed of every component in the processor.
This is why clock speed is such an important number and used as a yardstick for a computer’s performance. It’s measured in hertz (Hz), or cycles per second. Modern processors operate at a few GHz, or billion cycles per second. Every component needs to receive the clock signal at exactly the same time to maintain synchronisation. This means that the wiring connecting each component to the clock has to be the same length, creating a sort of fractal design that you can see when you look at a close-up photograph of a processor.
Putting a clock and flip-flops together, we have what is known as sequential logic. This can do everything combinational logic can do. In addition, it has the ability to store values and utilise them in later computation.
If you find the micro-architecture of digital circuits even slightly interesting, I highly recommend that you work through the first five chapters of nand2tetris (see further reading). If you really want to demystify the workings of your computer, there is nothing better than constructing one yourself!
The processor
We are now ready to learn how a computer is put together. Computers typically have a few key components. The processor is the component that decodes and executes binary-encoded instructions. Instructions and data needed for a program’s execution are held in memory. Since memory is volatile and cannot maintain its contents without power, a separate component, known as the hard drive, is needed for persistent storage. A computer will also include various input/output devices (e.g. keyboard, monitor, network card) so that the processor can communicate with the outside world.
The processor, or central processing unit (CPU), is the brains of the computer. It operates as a pipeline. Instructions go in one end, the processor executes them and the results of their computation come out at the other end. The processor operates an instruction cycle of fetching an instruction from memory, decoding it, executing it and finally writing back the output. The instruction’s execution will generate some output that changes the computer’s state e.g. writing a new value to memory. In doing so, it modifies the execution context of the subsequent instructions. Complex functionality is implemented by a succession of simple steps, each one building on the work of the last.
Our little ADD begins its exciting journey by being fetched from memory. When the user initialises a program, the operating system loads the machine code into memory and tells the processor where to begin. It keeps track of where the next instruction is by holding the instruction’s address in a special register called the program counter (PC). Normally, the processor moves sequentially through the instructions by incrementing the PC each time it executes an instruction. As we’ve seen, some instructions can jump to a new location by writing a new location to the PC. Once loaded from the hard disk, our instruction will sit patiently in memory waiting for the processor to work its way to it. Eventually, the value in the PC matches the location of our instruction and it is fetched from memory and transferred to the processor.
The processor now has our instruction in its maw. Before it can do anything, it must decode the instruction to understand what computation it specifies. Based on the design of the instruction set architecture, the processor will have circuitry that detects the instruction format and identifies the various fields within the instruction. The processor determines which registers it needs to use, the function specifier and so on. Within the processor is a component called the control unit that identifies and coordinates the bits of the processor that are needed to execute the instruction. When it decodes our ADD instruction, the processor will recognise that it needs to add two values together and it will identify where the values are held.
Finally, the processor is ready to execute the instruction. The control unit orchestrates moving the values from the inputs to the circuitry that performs the calculations to generate the output. To execute our ADD instruction, the control unit takes the values from the two registers and passes them to a component called the arithmetic logic unit (ALU). The control unit instructs the ALU to perform the requested addition. The ALU computes the result by passing the values to some adders and outputs the result. The control unit takes the value from the ALU’s output and writes it back into the destination register specified in the instruction.
And with that our little instruction has fulfilled its destiny! The processor fetches the next instruction and the whole circle of instruction life continues.
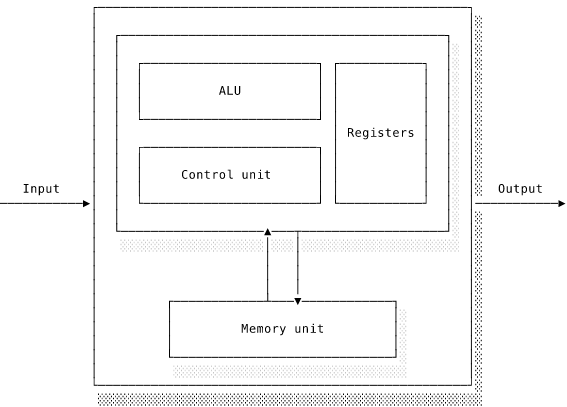
Let’s examine the components that make up the processor.
Registers
Registers are very small, very fast bits of memory located right in the processor itself. They hold the values the processor needs for the current instruction’s execution. Before the processor can operate on a value it must be loaded from memory into a register. After an instruction executes, the result is written back to a register. Processors typically have at most a few dozen registers and so making efficient use of them is very important.
Imagine that you’re studying in a library. The only books you can immediately refer to are the ones on your desk. You can return some books and withdraw other ones as your needs change, but you can only ever work with the books you have in front of you on your desk.
The control unit
The control unit is the component that coordinates work by sending appropriate signals to the rest of the processor. The control unit ensures that every other component receives the correct value at the correct time. Each component sits waiting for control signals that tell it what to do. The control unit is physically connected to the components via control lines, along which the control signals pass. I like to think of the control unit as an octopus with many tentacles worming their way in around all the components, triggering them all at just the right time to correctly perform the computation. The values themselves are passed around on buses, which are parallel rows of connections to allow multiple bits to transfer simultaneously.
The arithmetic logic unit (ALU)
The processor components that actually perform the execution are called execution units. The ALU is the execution unit that contains specialised circuitry for integer arithmetic (e.g. addition, multiplication) and logical (e.g. bitwise AND) operations. This is the real heart of the processor: it’s here that the actual computation happens. The ALU receives its input values, or operands, from the control unit along with an opcode extracted from the instruction. The ALU uses the opcode to activate the correct circuitry sections to perform the requested operation and outputs the result.
The ALU does not know or care where the operands come from or where the output should go. It is responsible purely for performing the calculations specified by its inputs. From the point of view of the control unit, the ALU is a black box. The control unit routes the inputs to the ALU, tells it what to do and then takes the ALU’s output for further processing. What we have here is a example of encapsulation within the processor.
In addition to outputting a value, the ALU can change its state by setting flags. These are normally stored in a special register, known as the status or flag register, in which each bit represents the presence or absence of a certain condition. It’s like a little set of switches squished into a byte. The ALU raises a flag by setting the flag’s corresponding bit to 1. This indicates that the relevant condition is present. To know what bit indicates what, you must refer to the processor’s programming manual. The exact set of flags varies from processor to processor but common conditions include whether the ALU output is negative, whether it’s zero and whether an operation resulted in a carry.
Subsequent instructions can command the processor to inspect the flags and execute the instruction only if certain flags are set. For example, a conditional branch might instruct the processor to only branch to a new location if the previous instruction raised the zero flag. Setting flags is a neat way to decouple the processor’s internal components. The ALU doesn’t need to know or care about which other components are interested in whether its result is a zero. It just sets the zero flag and moves on to its next task. Other components that do care can check the flag without having to directly monitor previous instructions.
Flags are also used for error handling. Attempting to divide by zero is a mathematical impossibility that a processor cannot compute. When asked to divide by zero, it must alert the rest of the system by raising a divide-by-zero flag. Error handling code will detect that the divide-by-zero flag has been set, interrupt normal execution and report it to the programmer. We’ll look at this “interrupt” process in much more detail in the operating systems chapter.
Floating point calculations are handled by a specialised floating point unit.
Memory
If an instruction’s output is immediately consumed by a subsequent instruction, it might stay in its register and never leave the processor. If we want to keep the output for later use, however, we need to write it out to the system’s main memory. A computer’s memory is the physical analogue of the Turing machine’s infinite tape. It is built from huge numbers of flip-flops, organised into bytes, that can maintain a value for as long as power is supplied. Memory is the computer’s working space, holding instructions and data that the processor needs to have accessible. All but the most simple processors interact with memory through a memory management unit (MMU). This is a component designed to work efficiently with the operating system to perform the calculations and look-ups that working with memory entails. We’ll explore how it works in the OS chapter.
Memory addressing
The size of the processor’s basic operating unit is known as the word size. This determines how many bits the processor can operate on at the same time and so specifies the size of the registers and buses. For example, a processor with a 32-bit word size will load 32-bit values from memory, store them in 32-bit registers and perform computation on 32-bit values. The exact size of a word will vary from architecture to architecture but will be a multiple of a byte. A few years ago there was a shift from 32-bit to 64-bit computers that completely bemused everyone non-technical. What that meant was that computers shifted from having a word size of four bytes (32 bits) to a word size of eight bytes (64 bits). The reason for doing so was to overcome limitations to how much memory a system could use.
The word size has important implications for memory. Each memory location must have a unique address, otherwise the computer would have no way of referring to the location. The number of unique addresses the computer can use is determined by how many bits the address size is. Typically, the address size corresponds to the word size. So on a 32-bit machine with 32-bit addresses there are 232 or 4,294,967,296 addressable memory locations. Over four billion seems large but it’s not in the context of computers. On x86 architectures each address refers to an individual byte value (known as byte-addressing). This means that a 32-bit computer can only address around four gigabytes of memory. There is simply no space in the address to refer to a location above that. It’s like trying to express the number 10,234 using only three digits – there’s no easy solution.
Various workarounds do exist, such as dividing a larger address space into segments and indexing into them using complicated addressing instructions, but this comes at a performance and complexity cost. Being able to address larger memory spaces was the main driver behind the switch from 32-bit to 64-bit machines. A 64-bit machine can address 264 locations, which corresponds to around 17 billion gigabytes. That should hopefully be enough for a while.
The memory hierarchy
An important characteristic of modern computers is that the memory operates at a much slower rate than the CPU. This is a fairly recent phenomenon. In the olden days, memory and processor operated at the same speed. Over the decades, however, increases in processor speeds vastly outpaced increases in memory speeds. Memory accesses are now a major performance bottleneck because the processor is forced to spend a lot of time waiting for the operation to complete. On a 3GHz processor, each execution step takes around 0.3ns (nanoseconds). Accessing a value in main memory might take around 120ns – 400 times slower!
The solution is caching. The principle is very simple. A program is more likely to reuse a recently accessed value than one it accessed a long time ago. This is called temporal locality. It makes intuitive sense if you think of how often computers iterate over the same set of values and operations. A program is also more likely to use a value if it’s located close to a previously used value, such as the adjacent elements in an array. This is called spatial locality. Processors can exploit temporal locality by holding recently used values in a small amount of very fast memory known as the cache. They can exploit spatial locality by caching values from adjacent addresses whenever they retrieve something from memory. If the program is accessing an array element, it is very likely to soon need the subsequent elements so it makes sense to pull in several each time.
When caching works well, the majority of values accessed are already held in the cache, greatly reducing the amount of time taken to retrieve them. The problem is that space in the cache is extremely limited. To be fast the cache must be small, which means that it can only hold a few values. Making the cache bigger makes it slower. To return to our library analogy, rather than returning books to the stack you could keep them easily accessible on a nearby set of shelves. They need to be small to be effective. The more books the shelves hold, the longer it will take you to find a particular book. The processor has to be very selective about what it keeps in the cache.
Modern processors use multiple caches to create a memory hierarchy. As we descend the hierarchy, each level offers bigger but slower storage. At the top of the hierarchy are the registers, which are the fastest but also smallest memory units in the system. Below them is the larger but slower level one (L1) cache. A modern L1 cache holds a few kilobytes. Below that is the L2 cache, holding a few hundred kilobytes, and below that the L3 cache, holding a few megabytes. Below the caches comes main memory itself. It’s markedly slower but can hold gigabytes of data. At the bottom, offering terabytes of storage but much slower speeds, is the hard disk.
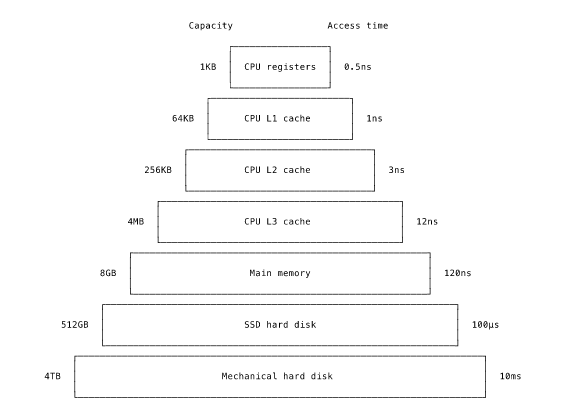
There are several algorithms for deciding what to keep in a particular cache and what to evict down to the next level. One simple approach is to let the cache fill up and then push out the least recently used value. For example, when a value in a register is no longer needed, it is moved from the register to the L1 cache. If it’s not used again, it’ll eventually get pushed out to the L2 cache and so on down the hierarchy. If a value falls to a lower level cache and is then reused, it moves back up to the top of the hierarchy. In this way, the most frequently used values stay at the top of the cache hierarchy and rarely used values move down to the lower levels.
When studying the performance characteristics of the memory hierarchy, I find it helpful to use a human-scale analogy. It can be hard to understand how nanoseconds and microseconds relate to each other. Instead, imagine that each processor step lasts for a single heartbeat. An L1 cache access then takes a few seconds. Enough time for a sip of coffee. An L2 access allows enough time, roughly ten seconds, for a yawn. An L3 access takes about forty seconds. That’s some twenty times slower than a L1 cache access but much faster than main memory. After initiating a main memory access, the processor would have to wait around five minutes for the response. You can see how avoiding even a few main memory accesses makes a huge difference. Even worse, accessing a SSD (solid-state drive) hard disk would take a couple of days and accessing a rotational hard disk would take months. Just for completeness, a 100ms network request would take several years to complete! Our poor processor could get a university degree in the time it would spend waiting.
Caching is completely transparent to the programmer. Processors generally don’t offer any instructions to query cache contents or to explicitly insert something into the cache. All you can do is measure how long it takes to retrieve a value and infer from that where it was stored in the memory hierarchy. When caching works well, it delivers average access speeds that are much faster than main memory accesses. The performance gains come at the cost of greater implementation complexity. The processor needs to have substantial circuitry to keep track of modifications to cached values and prevent stale values from being accessed.
Caching is a complex topic that crops up whenever there are time-expensive operations. We’ll come across it again when looking at networking. Many textbooks detail how to write “cache aware” code, meaning code that optimises its memory operations to keep the most important values in the cache. While processor caching is interesting, it’s important to keep things in perspective. As a web developer, the time cost of network operations is going to dwarf any performance gains you could possibly get from more cache aware code.
Performance optimisations
The picture I have presented in this chapter is deliberately simple. The processor described above executes one instruction at a time. This is wasteful. When the instruction is being fetched there is nothing for the decoder or execution units to do. The rest of the processor is stuck waiting. Common optimisations therefore introduce parallelism into the processor, allowing the processor to work on multiple things at once and reduce the amount of time components spend idle. These optimisations all add greatly to the complexity of the processor design, to the extent that it takes some effort to understand fully how a modern processor works.
Instruction-level parallelism tries to increase instruction throughput. Rather than executing one instruction to completion before starting the next, it is better to process the incoming instructions in a pipeline. For example, as the processor’s execution circuitry executes one instruction, the decoding circuitry can start decoding the next instruction. This increases the throughput without actually increasing how many instructions are executed at once. Modern processors feature deep pipelines of a dozen steps or more.
A pipelined processor still only handles one instruction at each step of the pipeline. An obvious optimisation is to widen the pipeline and allow multiple instructions at each step. Superscalar refers to pipelined processors that include multiple execution units (ALUs etc.) and so can process multiple instructions in parallel. The challenges now are keeping the pipeline as full as possible and working out which instructions can safely execute in parallel without changing the meaning of the program.
Conditional instructions create branch points where the processor has multiple possible execution paths. Processors use branch prediction circuitry to judge which path is more likely to be taken. The instructions from this path can be fed into the pipeline to keep it full without having to wait until the conditional instruction is executed. Branch prediction can sometimes be surprisingly straightforward. If your code contains an iteration such as for (i = 0; i < 1000000; i++) { ... }, the processor will quickly assume that the loop will continue to iterate. When the loop eventually finishes, the processor will have incorrectly predicted another iteration and will incur the cost of a branch mis-prediction. It will have to flush the pipeline of all the instructions and refill it with the instructions following the loop.
A processor may even perform out-of-order execution and reorder instructions if it determines that it can make more efficient use of the pipeline’s resources without changing the program’s meaning. This requires circuitry to detect any dependencies between the instructions and ensure that the reordering does not change the output.
Branch prediction is an example of speculative execution, in which a processor makes use of spare pipeline capacity to perform a computation that may or may not be needed in the future. If the computation turns out to be needed, the processor has saved time. If the computation isn’t needed, because the speculatively executed branch isn’t taken after all, the processor needs to be very careful to completely discard the work and revert any changes to the processor’s state. The recent Meltdown and Spectre security vulnerabilities were caused by processors not correctly removing cached values generated by speculatively executed instructions. That made it possible to infer the results of the instructions by determining which values were in the cache.
Instruction-level parallelism is good at executing a single task more quickly but even in superscalar processors the instructions need to share parts of the processor’s state. This means that it’s not possible to run two completely separate tasks at once. The logical progression is to achieve task-level parallelism, either by combining hardware support for multiple threads in a single processor (known as hardware threads), or by combining multiple, independent processors (now referred to as cores) in the same chip. So called multi-core processors are capable of performing truly independent tasks in parallel. Nowadays, consumer grade processors usually contain at least two or four cores and server chips might have four times as many. The shift to multi-core processors has huge implications for programming, which are the subject of the concurrency chapter.
The modern processor is a technical achievement of almost unbelievable complexity and ingenuity. It’s not a requirement that you understand all of this in depth. but I do encourage you to explore the further reading material to get a better sense of just how much stuff is going on in our phones and laptops. It’s really magical.
Conclusion
In this chapter we examined how computers operate as machines. We saw that all information is encoded in binary as a sequence of bits. We looked at the MIPS instruction set to better understand how this encoding might work. We saw how digital circuits perform logical computations by passing voltages through arrangements of transistors known as logic gates. These gates can themselves be arranged to form the simple components out of which more sophisticated elements are constructed. The most sophisticated component in a computer is the processor, which performs computation by decoding and executing machine code instructions. We followed an addition instruction through the processor and saw how the control unit, arithmetic logic unit and registers work together to compute a value. A component known as the flip-flop enables sequential logic and the construction of memory components that can remember previous values. Unfortunately, memory speeds have not kept pace with increasing processor speeds. One solution is to create a memory hierarchy containing multiple caches. Modern processors also include many complex optimisations designed to keep the processor’s execution units as busy as possible.
Further reading
Some of my favourite computing books are written about computer architecture!
Start with Code by Petzold (who also wrote The Annotated Turing, recommended in chapter one). It builds a foundational model of computing by starting from the absolute basics and gradually piling on the complexity. I still remember the revelation I had reading Code during a long coach journey. I suddenly realised that a computer is nothing more than lots and lots and lots of really dumb components working together. If you’ve ever thought to yourself “but how did the computer actually know that?”, then you need to read this book. Code explains from first principles how digital computers work in a gentle, didactic manner.
Next up is nand2tetris. It’s available as a free online course or as a textbook called The Elements of Computer Systems. In this book we take everything we learned in Code and write our own implementation. We start off designing logic gates and gradually work our way up to writing a complete computer system including the processor, assembler, compiler and operating system. Though challenging, it’s hard to overstate the satisfaction you get from really understanding how code is executed right down to the level of individual logic gates. The book itself is rather slim, which is why I recommend beginning with Code to make sure you have a good grasp of the concepts. The real value is in the projects so be sure to take the time to do them. It’s a popular course so you’ll have no trouble finding help online if you get stuck.
A limitation of nand2tetris is that we only implement simplified, toy versions of the components. This is intentional: implementing a modern processor would be an impossibly complex task. The danger is that we are left with an overly simplistic mental model that doesn’t reflect how things actually work. So, I advise you to continue your study at least a little further.
Computer Systems: A Programmer’s Perspective, by Bryant and O’Hallaron, is a wonderful textbook. As the name suggests, it approaches computer systems from the perspective of a programmer seeking to understand their system better. Exactly what we want! It’s my favourite textbook on computer architecture. The canonical textbook in this area is Computer Organisation and Design, by Patterson and Hennessy. It’s a bit more advanced than Computer Systems and focuses much more on the hardware implementation details. I particularly appreciated its in depth description of how a modern, superscalar, out-of-order processor works.
What every programmer should know about memory by Ulrich Depper is a wide-ranging treatment of memory in computing systems. I’d argue that it goes into significantly more depth than every programmer should actually know but at least chapters three and four, on CPU caching and virtual memory respectively, are important reading.
A fun way to learn about a particular architecture is to write some assembly code. You’ll learn about the architecture’s ISA and how to express functionality in low level code. You could write assembly for your PC, possibly with Randall Hyde’s The Art of Assembly Language, but this means starting off with the complex x86 instruction set. A simpler starting point could be an Arduino board, which uses the AVR instruction set. I found AVR Programming by Elliot Williams to be a very well-rounded introduction with some amusing project ideas. If you don’t want to muck around with buying hardware, the game TIS-100 is a fun way to get a taste of assembly programming.
Another great way to really learn an architecture is to write an emulator for it. An emulator is a program that imitates the physical behaviour of the emulated hardware. CHIP-8 is a simple architecture designed for easy emulation. From there, if you’re already a confident programmer, you could progress to a Nintendo NES or GameBoy.