Contents

Algorithms and data structures

Introduction

We have reached a state of piercing theoretical insight. In this chapter, we will apply our newfound analytical skills to commonly used algorithm and data structures. We’ll also briefly cover some abstract data types that will pop up in other chapters.

My approach here is going to be a bit different to what you’ll see in most textbooks on algorithms and data structures. They put a lot of emphasis on showing how to implement a wide variety of data structures and algorithms, usually in C. I don’t think that’s a particularly useful way for a self-taught person to start off. Learning how to implement a new data structure or algorithm in isolation is a sure way to immediately forget it. You need the reinforcement of regularly applying what you’ve learned to solve problems that you encounter daily. Computer science students have the luxury of being set problems and projects that test this new knowledge.

As a web developer, you’ll probably spend the majority of your time using the built-in data structures and algorithms provided by your language’s standard library or the browser environment. We’ll therefore focus on the data structures and core algorithms that are included in the languages and browsers you’re likely using every day. You’ll learn how they’re implemented and what their performance characteristics are.

I won’t spend any time on the fancy stuff behind the algorithmic brainteasers that some companies like to use for interviews. There are already many excellent interview preparation resources and there is no need for me to reinvent the wheel. As ever, the further reading section will have plenty of suggestions if you want to continue study.

Data structures

Look at any computer program and you’ll see two things: data and operations on that data. From the computer’s perspective, everything is just a huge sequence of ones and zeroes (i.e. bits, see the computer architecture chapter for more information). It is the programmer who creates meaning by telling the computer how to interpret these ones and zeroes.

Data types are a way of categorising the different forms of data a computer can utilise. A data type determines the (possibly infinite) set of possible values, the operations that can be performed on a value and maybe how a value can be physically implemented as a sequence of bits. Usually a programming language contains a few built-in, primitive types and allows you to make new types that build on the primitives. Common primitive types include integers, booleans, characters, floating point (i.e. decimal) numbers and strings.

Some data types are bound to a particular implementation. These are known as concrete data types. For example, the range of numbers that can be held by an int type depends on how many bits the underlying system uses to represent the number. A 64-bit int holds bigger numbers than a 32-bit int. Primitive types are nearly always concrete.

When a data type doesn’t specify an implementation, it is called an abstract data type (ADT). ADTs are merely descriptions of the set of possible values and the permitted operations on those values. Without an implementation you can’t create a value of the type. All you’ve done is specify how you’d like the value to behave and the computer doesn’t know how to create a value that behaves that way. I can want the moon on a stick but without a way of getting the moon on to a stick I’m not going to have it.

To actually use an ADT you need to create a data structure that implements the interface. A data structure defines a way of organising data that allows some operations to be performed efficiently. Data structures implement data types. Whether a particular data structure is a good implementation for a data type depends on whether the data structure efficiently implements the operations specified by the data type. The operations a data structure provides can be thought of as algorithms bound to the data held in the structure. We can therefore use the techniques we’ve seen above to measure the performance of a data structure’s operations and determine which tasks it is best suited to.

There exists a veritable zoo of data structures out there. In this section we’ll stick to the most fundamental ones: arrays, linked lists and hash maps. They’re incredibly useful and built-in to most programming languages.

Arrays

An array is the simplest possible data structure. It is a contiguous block of memory. That’s it. The array holds a sequence of identically sized elements. They have to be the same size so that the computer can know where the bits making up one element end and the bits making up another element begin. An array is therefore associated with the particular data type that it contains. The length, or size, of an array is determined by the size of the memory block divided by the element size. It indicates how many elements can fit into the array.

You can iterate through an array, by examining each element in sequence, or you can index, by jumping directly to any position in the array. We’re able to do this because the structure of the array allows us to work out the location of any element, provided we know the address of where the array starts and the element’s position within the array. Imagine that we have encoded the characters of the Latin alphabet into binary numbers that are two bytes long (a byte is eight bits). A array of size ten therefore requires a memory block twenty bytes long. We can immediately index any element in the array by calculating its memory address. We take the array’s base address (the address of the first element) and calculate an offset by multiplying the element size by the element’s index. If we assume our array of ten characters starts at memory address 1000, the addresses of the first four characters are as follows:

1 array[0] = 1000 + (0 * 2) = 1000
2 array[1] = 1000 + (1 * 2) = 1002
3 array[2] = 1000 + (2 * 2) = 1004
4 array[3] = 1000 + (3 * 2) = 1006

The strength of the array is its speed. Indexing an element in an array is a constant time operation. No matter how far away the indexed element is, we can always jump directly to it via a single calculation.

The simplicity of the array is also its main limitation. There is nothing in the structure of an array that marks the end of the array and so there is no way for the computer to know when it’s reached the end. In C a variable holding an array actually just holds the array’s base address. This means that the size of the array has to be stored in a separate variable and passed around with the array. The programmer is responsible for correctly updating the size variable when necessary. If you mistakenly tell the computer an incorrect size value, it will blithely iterate past the final element, possibly overwriting any values stored in those locations. This is known as a buffer overflow and is a major source of often very serious bugs. A second limitation of C-style arrays is that increasing the size of the array requires increasing the size of the allocated memory block. It’s often not possible to simply increase the size of the existing one because the adjacent memory addresses might already be in use. We frequently have to find a new, unused block of sufficient size and copy over all of the existing elements. Handling this manually is a bit of a pain.

More modern programming languages provide a slightly different data structure known as the dynamic array. They are so called because they have no fixed size, in contrast to static, C-style arrays. A dynamic array holds a raw array in a data structure that also keeps track of the number of elements in the array and its total capacity, thus preventing invalid indexing operations and removing the need to store the size in a separate variable. Dynamic arrays can resize automatically when they get filled up. If you don’t have to worry about the size of an array – as in Ruby, Python or JavaScript – you are actually using a dynamic array.

In many languages it’s hard to find out how a dynamic array actually works under the hood. In JavaScript, for example, there’s no simple way to get the current address of an array or any of its elements. This is by design: the whole point of dynamic arrays is to take this responsibility away from the programmer. Instead, let’s turn to Go. It offers an interesting intermediate point between the static arrays in C and the dynamic arrays in Ruby, Python and JavaScript. Go has C-style static arrays but builds on top of them another data structure, known as the slice, that works like a dynamic array. Go doesn’t hide any details of the underlying array. A slice is defined in the Go source code (runtime/slice.go) as a wrapper around an array:

1 type slice struct {
2         array unsafe.Pointer
3         len   int
4         cap   int
5 }

A pointer is a value that is the address of another value. It points to the value’s real location. A pointer can be dereferenced by accessing the value stored at the address held by the pointer. The slice doesn’t actually contain the array; it just holds the address where the array is. As well as the address of its underlying array, a slice tracks the len, the number of elements in the array, and the cap, the total capacity of the array. Let’s see them in action:

 1 package main
 2 
 3 import "fmt"
 4 
 5 func main() {
 6         slice := []byte{1, 2, 3}
 7         array := [3]byte{47}
 8 
 9         fmt.Printf("Slice %#v has length: %d and capacity: %d\n",
10                    slice, len(slice), cap(slice))
11         fmt.Printf("Slice element addresses: [%#p, %#p, %#p]\n\n",
12                    &slice[0], &slice[1], &slice[2])
13 
14         fmt.Printf("Array %#v has length: %d\n", array, len(array))
15         fmt.Printf("Array address: %#p\n\n", &array)
16 
17         fmt.Println("Appending another element...\n")
18         slice = append(slice, 4)
19 
20         fmt.Printf("Slice %#v has length: %d and capacity: %d\n",
21                    slice, len(slice), cap(slice))
22         fmt.Printf("Slice element addresses: [%#p, %#p, %#p, %#p]\n",
23                    &slice[0], &slice[1], &slice[2], &slice[3])
24 }

This program defines a slice and initialises it with three values. Immediately afterwards, we define a static array of size 3 but with only one initial value. Here is the output:

1 Slice []byte{0x1, 0x2, 0x3} has length: 3 and capacity: 3
2 Slice element addresses: [c000086000, c000086001, c000086002]
3 
4 Array [3]byte{0x2f, 0x0, 0x0} has length: 3
5 Array address: c000086003

The addresses are written in hexadecimal. Even though array only contains one actual value, space for two more has already been allocated. Notice that the elements held by slice are all adjacent to each other in memory and the address of array comes directly after. That means there is no empty space between the two variables. What do we expect to happen when we append another element to the slice? We know that the slice is a wrapper around a static array with a capacity of three. There won’t be room for a fourth element. We can’t just expand the underlying array because the memory address it would use is already occupied by array. We therefore expect that Go will have to find a new, bigger memory block for slice and move all the existing elements. Sure enough:

1 Appending another element...
2 
3 Slice []byte{0x1, 0x2, 0x3, 0x4} has length: 4 and capacity: 8
4 Slice element addresses: [c000086030, c000086031, c000086032, c000086033]

The elements all have new addresses because they have been reallocated to a different block of memory. Go allocates a bit of extra space, raising the capacity to 8, to allow more elements to be appended without having to immediately resize again. It’s common for dynamic arrays to increase their size by a large amount whenever they reallocate because reallocations are expensive and it makes sense to try and minimise how many are needed.

A consequence of having all the elements adjacent to each other is that inserting an element at the beginning or a point in the middle of the array requires shuffling every subsequent element along to make space. Deleting an element entails shuffling in the other direction to fill the gap. This gives us the following performance summary:

operation	performance
index	O(1)
insert/delete at beginning	O(n)
insert/delete at middle	O(n)
append	O(1) amortised

Appending an element only causes a reallocation if the array is full. This makes it a bit tricky to work out the performance of appends because it can vary a lot depending on whether a reallocation is needed. Rather than saying that most appends are constant but those that trigger a reallocation are linear, we average out or amortise the cost of reallocation across all append operations. Amortised in this way, the cost of the occasional reallocation becomes negligible and we say that appending is a constant operation.

Linked lists

We’ve seen that arrays are contiguous blocks of memory of a fixed length. Increasing the size of the array requires reallocating the elements to a new, bigger memory block. It is possible to overcome this limitation by building a dynamic array on top of a static one. A completely different approach is the linked list. It’s an extremely simple, recursive data structure in which each element contains a value and a link to the next element. The first element is known as the head and all of the following elements are the tail. The structure is recursive because the tail is itself a linked list with a head and a tail.

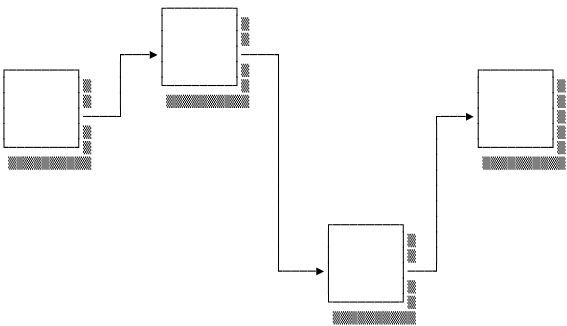
The “link” in each element is a pointer to the next element. If you have the head, you can iterate through the whole list by following the head’s pointer to the next element, then the next pointer to the following element and so on. Because we explicitly record the elements’ addresses they don’t need to be next to each other in memory. In fact, they can be stored anywhere. This makes it easy to insert or delete elements. There’s no need to maintain a contiguous memory block and reallocate when it’s full. Insertions and deletions can be performed in constant time by rewriting the pointers in the surrounding elements. In the diagram below you can see how most of the elements are unaffected by the insertion of a new element:

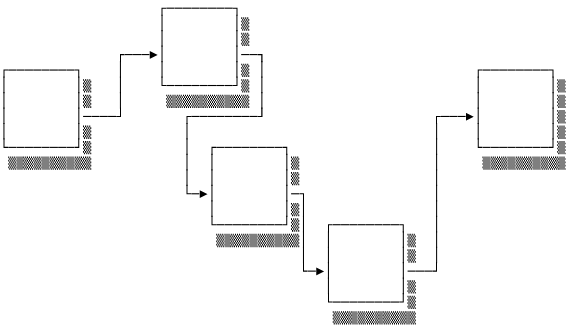
However, to insert or delete an element in the middle or end of the list we first need to find the preceding element. The strength of the linked list, its explicit addressing, is also its downside. Since we have no idea where a particular element might be in memory, we need to iteratively follow each pointer from the head until we get to the element. This means that accessing an element in a linked list is a linear time operation. The access time needs to be factored in when considering insertions and deletions that aren’t at the head of the list.

Linked lists are particularly popular in functional programming languages such as Haskell, mostly for reasons of convention and style. Functional languages, which we’ll see more of in the chapter on programming languages, prefer to use recursion over explicit iteration with loop counters and so on. The recursive structure of the linked list fits this nicely. In Haskell you move through a list by splitting a list into its head and tail and recursively repeating the process on the tail. Here is an example of searching for a character in a list:

1 find :: [Char] -> Char -> Bool
2 find haystack needle =
3   case haystack of
4     [] -> False
5     head : tail -> if head == needle then True else find tail needle

haystack is a list of characters and needle is the character we are looking for. In the case structure we check what haystack contains. If it’s an empty list ([]), it clearly doesn’t contain what we’re looking for and we can return False. Otherwise, we use the head : tail syntax to pull the head off the list. If it’s a match, we return True. If not, we recursively call find with the tail. Each time we call find we peel off the first element from the list and haystack gets smaller and smaller. Eventually, we either find the value or end up with an empty list. And to prove that it works:

1 > find ['a', 'b', 'c'] 'b'
2 True
3 > find ['a', 'b', 'c'] 'd'
4 False

Indexing an element in an array is a constant time operation but insertion or deletion is linear due to the shuffling required. For linked lists it’s the other way around. Indexing is a linear operation but making the actual insertion or deletion is constant once the element has been accessed. A simple optimisation for appending is to maintain a pointer to the final element in a variable. This gives direct access to the end of the list and avoids needing to iterate through the whole list to reach it.

operation	performance
index	O(n)
insert/delete at beginning	O(1)
insert/delete at middle	access time + O(1)
append	O(n), O(1) if end known

The lists we have seen here are known as singly-linked lists because each element holds only a single link: the address of its successor. If you want to find an element’s predecessor you have to search from the beginning. The links in the chain only go one way. In a doubly-linked list each element also contains a link to its predecessor, which makes it possible to move back up the list at the cost of having to store two addresses per element instead of just one. Whether the extra space overhead is worth the speed improvement depends on the size of the elements and how the program uses the linked list.

Hash maps

Sequential data structures have many uses but the only way to refer to an element is by its index. Very often we want to refer to a value by its name or some other identifier that we shall call its key. To get this functionality we need the hash map. This data structure stores elements as key-value pairs and allows the user to retrieve a value using its key. Hash maps go by a variety of names. In Ruby they’re called hashes, in Python they’re dictionaries and in JavaScript they’re objects. The slight differences between each implementation aren’t important for us.

Hash maps are so-called because they rely on hashing. This is one of those computer science things that pop up a lot and sound very complicated but actually aren’t. A hash function maps an input to an output within a given range. For example, string.length() % 5 will convert all strings to a number between zero and four. It’s important that the function is stable and always gives the same output for the same input because that creates a reliable mapping between the input and the output. Ideally, a hash function will distribute the inputs evenly across the range of output values. Coming up with good hashing functions is a tricky mathematical problem. Happily we can leave that to one side and simply rely on existing implementations.

A hash map uses a hash function to convert the key into an integer that is then used as an index into an array. Each array element is referred to as a bin that holds a value. The hash function maps the key to a location in the array, making the key a kind of indirect index into the array. As we insert more values into the hash map, we will most likely encounter collisions where two different values are hashed into the same bin. A common solution to this problem is to put both values into a linked list and store that list in the bin. When we want to retrieve an element, we hash the key to find the bin as usual and then iterate through the list until we find the desired element. So the hash map is itself built out of the two data structures we’ve already seen!

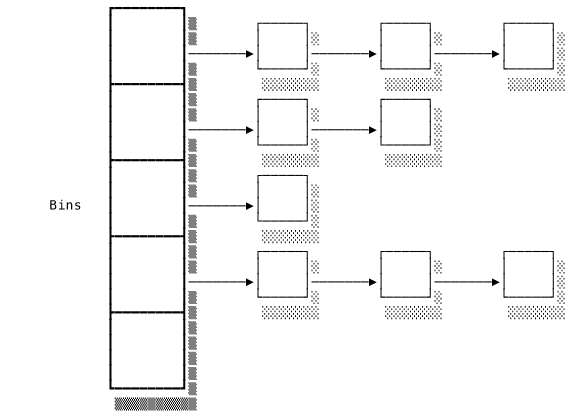
When everything’s going well, hash maps offer constant time performance. The only significant cost is performing the hashing operation. However, a hash map’s performance can become degraded if the hash function puts too many elements into a single bin. If too many values end up in just a few bins, the hash map spends most of its time iterating through the lists and becomes a glorified linked list. As we know from the previous section, iterating through a linked list is a linear operation. A good hash map implementation will detect when the lists are getting too long and amend its hash function to redistribute the values over a larger number of bins. An occasional resizing keeps the lists short and ensures good performance. The cost of the resizing is amortised.

For an in depth analysis of how Ruby implemented a hash map similar to the above, I highly recommend Ruby under the microscope (see further reading). Ruby’s implementation has changed somewhat since the book’s publication but it’s still well worth a read. In the further reading is a Heroku blog post giving a good overview of the changes that came with Ruby 2.4.

Abstract data types

An abstract data type is a data type without an implementation. They are useful because code using them doesn’t have to know or care about the details of the implementation. If you find a more suitable implementation of the interface, you can swap it with the old one without having to modify any consuming code. As an example, see below how Java handles the List interface.

We’ll briefly review some important abstract data types and how they can be implemented with the data types we’ve seen. We’ve only seen three data structures, but that’s already enough to implement a few interesting ADTs. I’ll capitalise the names of ADTs to distinguish them from data structures, which are uncapitalised.

The Array ADT is an ordered collection of elements with two operations:

1 get(array, index) // returns value at index
2 set(array, index, value) // writes value to index

The List ADT is an ordered collection of elements with three operations:

1 cons(value, list) // prepend value as new head
2 head(list) // returns head of list
3 tail(list) // returns tail of list

Don’t worry if you find the distinction between Arrays and Lists confusing. They are very similar but have a difference in emphasis. The operations specified by the Array prioritise indexing anywhere in the Array, which favours an array data structure, while the operations specified by the List prioritise manipulating heads and tails, which favours linked lists. Partly it’s a question of history. Lists originated with the programming language Lisp, which used linked lists (and is from where the cons term comes). The situation is more confused nowadays because Lists and Arrays seem to be almost synonymous. The Array ADT in JavaScript and the List interface in Java specify very similar sets of methods that combine operations from both.

One nice thing about Java is that it makes the distinction between a data type and a data structure clear when you initialise a variable. In Java ADTs are defined as interfaces, which are literally a set of method signatures that an implementing data structure needs to provide. It is not possible to directly create an interface. You need to create a data structure that implements the interface. In Java this is done by instantiating a class using new. Here’s how you create a List of strings implemented by an array:

1 List<String> myStringList = new ArrayList<String>();

ArrayList is Java’s name for a dynamic array. If you notice that your program spends a lot of time adding new elements to myStringList but rarely indexes into it, you can change the implementation to use a linked list simply by instantiating a different class:

1 List<String> myStringList = new LinkedList<String>();

The variable’s type remains List<String> and so you can swap the implementing data structure without having to change the data type.

We already encountered the Stack in the previous chapter. To recap, a Stack is a collection of elements with two operations:

1 push(stack, value) // add value to collection
2 pop(stack) // remove most recently added value

A peek operation, exposing the top value without removing it, is often present too. The Stack operates on the principle of last-in, first-out (LIFO). Stacks appear throughout computer science and we’ll encounter them again numerous times in this book. They’re particularly well suited to managing nested operations that exhibit LIFO behaviour. A Stack can be implemented with arrays or linked lists.

A Queue is another collection of elements with two operations:

1 enqueue(queue, value) // add value to back of queue
2 dequeue(queue) // remove value from front of queue

The Queue is so named because it provides first-in, first-out (FIFO) behaviour. It’s just like a queue of people. As you might expect, Queues are used when it’s important to process elements in the order in which they’re added. Queues can be efficiently implemented by linked lists (single or double) as long as there is a reference to the final element as well as the head. They can be implemented by arrays with one index representing the head and another representing the final element. When an element is enqueued or dequeued the indexes are adjusted, wrapping from the end of the array back to the beginning if necessary. This avoids having to shuffle the values in the array.

A super cool and useful ADT is the Tree. Conceptually a Tree looks like this:

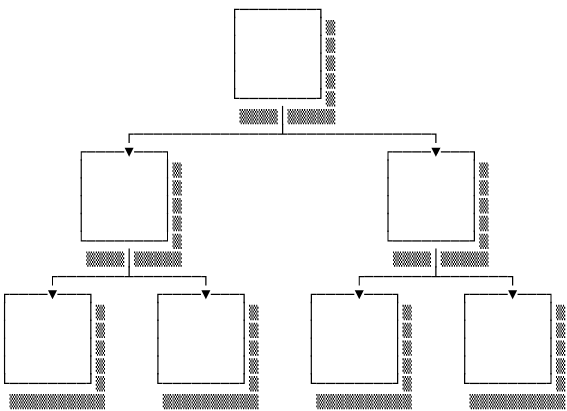
A Tree consists of a root node (the one at the top) with zero or more child nodes. Two nodes cannot have the same child. The structure is recursive because each child forms the root of its own subtree. The minimum necessary operations are therefore really simple:

1 value(node) // get value held in a node
2 children(node) // get child nodes from a node

One way of implementing a Tree is as a linked list where each element in the list can have zero or more pointers to other elements. In this view, a linked list is just a special Tree where every node has a single child.

Trees appear in many areas of computer science. They’re an obvious natural fit for data with hierarchical relationships. A very useful variation is the binary search tree (BST). In a BST each node has at most two children. All of the values in the left subtree will be less than the current node’s value and all of the values in the right subtree will be greater than the current node’s value. A BST is structured so that traversing it is equivalent to a binary search, which we will look at in the next section.

Finally, a Graph is a Tree in which multiple nodes can point to the same child. It ends up more like a web of relationships:

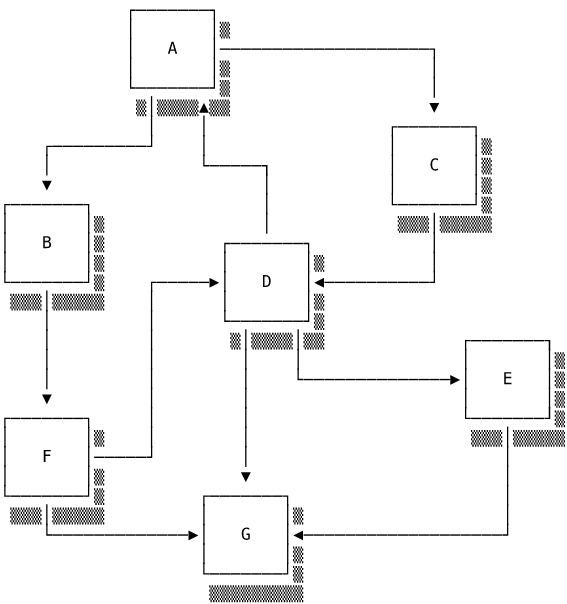
In the world of Graphs, the nodes are called vertices and the links between them edges. Graphs are very useful any time you need to model the relationships between elements. In an undirected Graph an edge between A and B implies a relationship both from A to B and from B to A. In a directed Graph the edges are more properly called arrows and only go in one direction. A social network might use a Graph to model the web of friendships between its users. An undirected Graph would only indicate friendship but a directed Graph could additionally indicate who “friended” whom on the website.

When there is a value associated with each edge or arrow, the Graph is weighted and unweighted if there is not. If you modelled towns as vertices, the edges between them could be weighted with the distance between each pair of towns. Finding the shortest route between two towns could then be solved by finding the path between the two vertices with the lowest total weighting. The Graph above is an unweighted, directed Graph.

Traversing a Graph is trickier than traversing a Tree because of the possibility of cycles: vertices that connect together in a loop. In the example above there are two cycles: A-B-F-D-A and A-C-D-A. When traversing a Graph, you must keep track of which vertices you have already visited to avoid infinitely looping around a cycle. A directed, acyclic Graph (DAG) has directed edges with no cycles. DAGs are commonly used to model different kinds of information with dependencies e.g. family trees and package manager dependencies.

A straightforward implementation of a Graph is via an adjacency list. Vertexes are stored in a list and every vertex stores a list of the vertices it is adjacent to. There are many different ways of implementing Graphs, and indeed many ways of implementing adjacency lists, each with different performance trade-offs.

It’s hard to overestimate how important Trees and particularly Graphs are in computer science. Graphs even have their own branch of mathematics called – you guessed it – graph theory. A vast number of concepts can be efficiently modelled with Trees and Graphs, sometimes in surprisingly elegant ways. In this short section I don’t have enough space to do anything but whet your appetite. I strongly encourage you to check out the resources in the further reading section and explore these fascinating data types further.

Algorithms

An algorithm, as we saw in the previous chapter, is a sequence of instructions to carry out computation. A computer program is an algorithm written in code that the computer can understand. We’ve already seen how to perform algorithmic analysis and work out the performance characteristics of algorithms. In this section we’ll look at two very important classes of algorithms: sorting and searching. I’ve chosen to focus on just these two because they are so fundamental to solving everyday programming problems but are also complex enough to demonstrate a range of design approaches.

Sorting

A sorting algorithm takes a collection of items and arranges them according to some ordering rule e.g. alphabetically or by size. Sorting is a fundamental operation because we often want to be able to impose an order on values. In addition, we can solve some problems with more efficient algorithms if we can provide a sorted input. There is no single best way to sort an input. Different algorithms perform differently, depending on factors such as the size of the input and how the values are distributed (is it mostly sorted already? Is it in reverse order?). Each algorithm will have different time and space requirements for different inputs. An algorithm that is optimal for sorting a small collection of values could be completely unsuitable for sorting very large collections.

The standard textbook approach is to prove the complexity of an algorithm and then implement it in C. I want to take a slightly different approach here. I’m assuming that you program in an environment that already includes fast sorting methods or functions. It might be intellectually interesting to implement a sorting algorithm yourself but you’re vanishingly unlikely to ever need to do so in real code and so you’ll quickly forget. I know that this has certainly happened to me (a few times!). Instead, we’ll look at things from the other direction and see how some important applications choose to implement sorting. We’ll dive down in the implementation of JavaScript sorting in Firefox and Chrome. We’ll see which algorithms they chose, the performance implications and the trade-offs involved. My hope is that this approach will give you a more intuitive understanding of how sorting works.

Browsers have a lot of leeway in how they implement JavaScript. The specification only requires that it sorts in place by modifying the input array and that the default sorting method is lexical (i.e. alphabetical). Since lexical sorting is pretty useless, Array.sort also takes an optional compare function. If compare(a, b) returns less than zero, then a is sorted before b and vice versa:

1 [1, 15, 2, 3, 25].sort()
2 > [ 1, 15, 2, 25, 3 ]
3 [1, 15, 2, 3, 25].sort((a, b) => a - b);
4 > [ 1, 2, 3, 15, 25 ]

As long as a browser implements this functionality, it can use whatever sorting algorithm it chooses. So, which ones do they choose and why?

If you dig into the Firefox source code you’ll see that it uses merge sort. Merge sort is a recursive algorithm that uses a design paradigm known as divide and conquer. We’ll see other examples below. The idea behind divide and conquer is that you can more simply solve a problem for a large input by breaking it down into smaller sub-problems, solving those sub-problem and then combining each sub-result into the overall solution. Divide and conquer algorithms are often implemented using recursion.

Merge sort is based on the observation that it’s easy to merge two sorted lists. You just compare the first element of each list, extract the lowest, add it to a new list and repeat until both inputs are empty. The algorithm works by recursively dividing the input into sublists, known as runs, until the runs only contain one element each. It then merges the two single-element runs into a sorted two-element run. Next, it merge those two runs to create a four-element run. It continues until the runs are all merged together into the final, sorted output. The algorithm’s name comes from the fact that the sorting is actually performed when merging the runs. A Python implementation might look like this:

 1 def merge_sort(input):
 2     if len(input) <= 1:
 3         return input # a run with one element is sorted
 4 
 5     middle = len(input) // 2
 6     left = input[:middle]
 7     right = input[middle:]
 8 
 9     left = merge_sort(left)
10     right = merge_sort(right)
11     return list(merge(left, right))

The recursive calls to merge_sort break the input down into smaller and smaller runs until they only hold a single element. Then each call uses merge to construct a sorted list out of left and right. Since we can rely on left and right always being sorted (a list of one element is sorted!), merge can easily construct a new sorted list by repeatedly pulling the lower of the two elements from the heads of left and right.

Merge sort offers reliable O(nlog(n)) time performance, which is very good for sorting algorithms. Its weakness is that when performed on arrays it requires a linear amount of memory to store all the runs it generates, though various optimisations exist. This is not such a problem with linked lists. In fact, merge sort is well suited to linked lists because it only ever needs to access the head of each list. Finally, merge sort scales well to huge inputs that don’t fit in memory. To sort such an input, divide it into chunks that do fit in memory. Sort each chunk in memory and write the sorted output to a file. Then merge each sorted file together by the same process above to create the final output.

Another advantage of merge sort is that it is stable. Assume I have a list of JavaScript objects representing users with age and surname properties. Many users with different surnames will share the same age. I sort them first by surname and then by age. If the algorithm is stable, I will have a list of users sorted by surname and then, within each surname grouping, sorted by age. If the algorithm is unstable, then the users will be sorted only by age and no longer by surname. The benefit of a stable sort is that we can “stack” sorts by applying them one after the other. If the sort isn’t stable we can’t do this. The JavaScript specification does not currently require a stable sort but this will change in an upcoming revision. It’s pretty clear why Firefox (and Safari, incidentally) use merge sort: it’s reliably efficient and stable.

Next up is Chrome, which uses the V8 JavaScript engine. Before v7.0, the V8 engine had a particularly interesting implementation of Array.sort():

 1 function ArraySort(comparefn) {
 2   var array = TO_OBJECT(this);
 3   var length = TO_LENGTH(array.length);
 4   return InnerArraySort(array, length, comparefn);
 5 }
 6 
 7 function InnerArraySort(array, length, comparefn) {
 8   // In-place QuickSort algorithm.
 9   // For short (length <= 10) arrays, insertion sort is used for efficiency.
10   function QuickSort(a, from, to) {
11     // ...
12     while (true) {
13       // Insertion sort is faster for short arrays.
14       if (to - from <= 10) {
15         InsertionSort(a, from, to);
16         return;
17       }
18       // do Quicksort instead...
19     }
20     // ...
21   }
22   QuickSort(array, 0, num_non_undefined);
23 }

ArraySort calls into InnerArraySort, which calls into QuickSort, which then actually decides to call InsertionSort for short inputs. To understand why V8 does this, we need to look at the performance of the two algorithms.

Insertion sort is a very simple algorithm. The process is similar to how many people sort a hand of cards. Since I’m left handed, I designate the leftmost card to be the first sorted card. I then take each card from the unsorted section and insert it into the sorted section in the correct position. Eventually, all cards are sorted. An implementation in code iterates through the input and moves each element to the correct location in the output. This could be an entirely new array or, more commonly, the algorithm shuffles the elements of the input around to keep the sorted ones at the beginning. This means that the algorithm doesn’t require any extra memory. Here is a neat solution in Go:

 1 func insertionSort(a []int) {
 2     for i := 1; i < len(a); i++ {
 3         value := a[i]
 4         j := i - 1
 5         for j >= 0 && a[j] > value {
 6             a[j+1] = a[j]
 7             j = j - 1
 8         }
 9         a[j+1] = value
10     }
11 }

Note that this implementation designates a[0] as the first element of the sorted output. At each iteration, the outer loop increases the size of the sorted section and assigns the newly included element to value. The inner loop moves down through the sorted section and ensures that value ends up in the correct position. This maintains the sorting. The nested for loops should tell you that insertion sort’s average time performance isn’t that great: O(n²). At least insertion sort is stable.

Insertion sort’s quadratic performance is much slower than Quicksort, a venerable algorithm that has been in the C standard library for decades. Quicksort is another example of a recursive, divide and conquer algorithm. Quicksort works by dividing the input into two sections around a pivot. Values that are bigger than the pivot are moved above it and values that are smaller are moved below. All of the values in the top section are now greater than all of the values in the bottom section but each section needs to be internally sorted. The algorithm recursively calls itself on the two sections until everything is completely sorted. At each step, the size of the problem is halved (in the best case where the value of the pivot is exactly in the middle of the input range). This is characteristic of divide and conquer algorithms. Its implementation in Haskell is remarkably clear:

1 qsort [] = []
2 qsort (x:xs) = qsort [y | y <- xs, y < x] ++ [x] ++ qsort [y | y <- xs, y >= x]

Remember that x:xs means x is the head of the list and xs is the tail (i.e. every other value). As described above, we set x to be the pivot. You can see it in the middle. Below the pivot, we use [y | y <- xs, y < x] to make a list of every value from xs less than x. Above the pivot, we make another list of values greater than or equal to x. We recursively call qsort on the two sections and concatenate the results to the pivot using ++.

Quicksort usually offers O(nlog(n)) performance but can degrade to O(n²) performance when the pivot value happens to be the smallest or largest value in the list. That creates one section holding only one element and another nearly as long as the original input, rather than creating two sections equal to half of the original. Recursively dividing the problem into smaller sub-problems is logarithmic in nature and so Quicksort will make log(n) function calls. As we’ll see in the operating systems chapter, each function call consumes some memory, so Quicksort has O(log n) space requirements.

If Quicksort’s worst-case performance is the same as insertion sort’s best-case performance, why did V8 use insertion sort at all? Insertion sort does have something to bring to the party. It performs very well on small inputs, when even a quadratic algorithm performs quickly. When the input size is small, the amount of time spent actually sorting is overwhelmed by the overhead of the recursive function calls in divide and conquer algorithms like Quicksort or merge sort. Insertion sort doesn’t need to use recursion and so avoids the overhead. I think this is a great example of why we should take care not to put too much emphasis on big-O notation. It’s very approximate and actual performance can be different, especially with small input sizes. The V8 team did their measurements and found that the best way to handle the disadvantages of both algorithms was to use them in concert.

Unfortunately, this pedagogical case study is no more. The problem with Quicksort is that it is not stable. Calling Array.sort() in Chrome would give different results to other browsers that used stable sorting algorithms. The V8 team were keen to use a stable sorting algorithm for consistency but wanted to keep the performance they had achieved with their insertion/Quicksort combo. Their solution was to switch to TimSort, an engagingly-named but vastly more complex algorithm. The team wrote a very interesting blog post about the transition.

TimSort is also the sorting algorithm used by Python. A quick look at Ruby’s source code reveals that Array#sort! uses Quicksort:

 1 VALUE
 2 rb_ary_sort_bang(VALUE ary)
 3 {
 4     // loads of stuff ...
 5     VALUE tmp = ary_make_substitution(ary);
 6     struct ary_sort_data data;
 7     long len = RARRAY_LEN(ary);
 8 
 9     RARRAY_PTR_USE(tmp, ptr, {
10         ruby_qsort(ptr, len, sizeof(VALUE),
11         rb_block_given_p()?sort_1:sort_2, &data);
12     });
13 
14     // loads more stuff...
15 }

The C code is pretty hard to read but you can see the call to ruby_qsort lurking in there, which in turn calls out to the operating system’s Quicksort implementation or falls back on its own.

And finally, here is a summary of the algorithmic complexity of the three sorting algorithms we’ve seen. From our survey of browser implementations, we know that big-O notation is not the last word on performance. Nevertheless, it’s useful to have a rough idea of how the algorithms perform:

Algorithm	Best case	Average case	Worst case	Space requirements	Stable?
Quicksort	O(n log n)	O(n log n)	O(n²)	O(log n)	no
Merge sort	O(n log n)	O(n log n)	O(n log n)	O(n)	yes
Insertion sort	O(n)	O(n²)	O(n²)	O(1)	yes

Searching

A search algorithm looks through an input, known as the problem domain or problem space, to find a solution. The problem domain might be an actual list of values provided to the algorithm but it might also be more abstract, such as the set of possible configurations of a chess board. In this section, we’ll stick to the straightforward meaning of looking through an input collection to find a specified value. There are two main approaches: linear and binary search.

A linear search is the most straightforward way of finding something. You start at the beginning and iterate through to the end, checking each value as you go until you either find what you’re looking for or reach the end of the input. As you might have guessed, a linear search offers linear performance. A second attribute of the algorithm is that it will always find the first matching value. This is super useful with pre-sorted inputs. For example, to find the first occurrence of an error message in a list of log messages you could sort by timestamp and then perform a linear search for the error message.

Ruby’s Array#any? method is an example of linear search:

 1 static VALUE
 2 rb_ary_any_p(int argc, VALUE *argv, VALUE ary)
 3 {
 4     // ...
 5     else {
 6         for (i = 0; i < RARRAY_LEN(ary); ++i) {
 7             if (RTEST(rb_yield(RARRAY_AREF(ary, i)))) return Qtrue;
 8         }
 9     }
10     return Qfalse;
11 }

The function is implemented in C, so it’s a little hard to read, but you can see that it iterates through the input array and tests each value, returning QTrue as soon as it finds a match.

Can we improve on linear search? If the input is unsorted, there’s not really much we can do. We cannot make any assumption about where in the input our sought after value might be. If we had a sorted input we could make educated guesses about where the value might be. Take the example of a dictionary. If you’re looking for the word “sort”, you don’t start at the beginning and look through every page. You know that words beginning with “s” are going to be towards the end and so you open the dictionary at roughly the right place. If you overshoot on either side you compensate by moving a little bit in the other direction and repeat the process until you land on the right page. That is how binary search works.

Expressed as an algorithm, it compares the value to the midpoint of a sorted input. If they match, the value has been found. If the value is greater than the midpoint, then the algorithm recursively calls itself on the top half of the input. If the value is smaller, then it calls itself on the bottom half. At each step, the algorithm halves the search space by discarding values that it knows can’t contain the value. This should be ringing some bells in your mind. It’s a divide and conquer algorithm, just like Quicksort! The binary search tree we saw previously a data structure designed so that traversing through it is equivalent to performing a binary search. It’s a neat example of how a data structure can be designed to optimise for specific operations.

Since it’s a divide and conquer algorithm, binary search has logarithmic time performance. Although much faster than a linear search, this comes at the cost of requiring the input to be sorted. Whether it is better to perform a linear search or first sort and then perform binary search will depend on the size of the input and how many searches are required.

Ruby offers its own implementation of binary search in the form of Array#bsearch:

 1 while (low < high) {
 2     mid = low + ((high - low) / 2);
 3     val = rb_ary_entry(ary, mid);
 4     v = rb_yield(val);
 5     // ...
 6     if (rb_obj_is_kind_of(v, rb_cNumeric)) {
 7         const VALUE zero = INT2FIX(0);
 8         switch (rb_cmpint(rb_funcallv(v, id_cmp, 1, &zero), v, zero)) {
 9           case 0: return INT2FIX(mid);
10           case 1: smaller = 1; break;
11           case -1: smaller = 0;
12         }
13     }
14     // ...
15     if (smaller) {
16         high = mid;
17     }
18     else {
19         low = mid + 1;
20     }
21 }
22 if (!satisfied) return Qnil;
23 return INT2FIX(low);

I’ve tried to cut out all but the essential code showing how the algorithm works. You can see that it compares the midpoint to the search value (in the switch statement) and redefines the high and low limits of the search space accordingly.

Binary search is an example of a more general optimisation technique known as hill climbing. Imagine that the answer we’re looking for is on the summit of a hill. We are on the side of the hill but thick fog hides the summit. Even if we don’t know where the summit is, a sensible assumption would be that going up the hill will take us closer to the summit. Binary search does something similar when it compares the sought after value to the midpoint. At each iteration the algorithm can halve the size of the problem space by selecting the half that must contain the value.

Hill climbing is a useful technique when you need to find a good solution to an NP-complete problem. The excuse “sorry, that’s intractable” isn’t going to wash with your non-technical manager so you need to come up with something that gets close to the optimum. To apply the hill climbing technique, first generate any correct solution. For example, if you’re dealing with the travelling salesman problem, just find any valid route that goes through all of the towns. Then make a single change, such as swapping around two towns. Does that lead to a better or worse solution? If worse, undo it. If better, keep it and now make another change. Gradually, over repeated iterations, the algorithm produces an improved solution that approximates the optimum. It’s unlikely to be the optimal one but it can get very close in a short time.

Conclusion

In this chapter we looked at the distinction between data types and data structures. We saw that data structures implement data types. We examined some fundamental data structures – the array, linked list and hash map – and analysed their performance characteristics. We saw how dynamic arrays are constructed from static arrays, using Go as an example. We then reviewed some very important abstract data types and got a sense of how they can be implemented and the problems they solve. We then examined and compared the implementation of JavaScript sorting algorithms in the major browsers. Finally, we finished off by looking at the two main ways of performing searches, linear and binary, and saw how the Ruby standard library implements both. We saw that divide and conquer algorithms work by splitting a large problem into many smaller ones, often leading to more efficient solutions. Binary search is an example of a more general optimisation technique known as hill climbing.

And with that we reach the end of the theory! I hope you found the theory interesting but if you’re itching to start more practical topics, read on. Our next step is to apply theory to reality and get into the nuts and bolts and bits and bytes of real computers.