Contents

Programming languages

Introduction

A programming language is a language designed for specifying programs. We instruct computers to understand these languages and perform the computations they specify. The branch of computer science that studies programming languages is known as programming language theory (PLT). It sits at a really interesting intersection of computing, linguistics, logic and mathematics.

The standard academic analysis of programming languages generally involves working up from logical first principles. We’ll approach the subject from the other direction by making a survey of a few popular programming languages. We’ll begin by looking at how programming languages can be understood in terms of their syntax and semantics. Then we’ll examine how they can be categorised into different paradigms according to a few important, distinguishing features. Type systems are important and interesting enough to merit their own section at the end of the chapter.

Let’s begin our survey by looking at what Wikipedia has to say about JavaScript, Go and Haskell, three popular and distinctive languages:

JavaScript is a high level, just-in-time compiled, object-oriented programming language that conforms to the ECMAScript specification. JavaScript has curly-bracket syntax, dynamic typing, prototype-based object-orientation, and first-class functions.

Go is a statically typed, compiled programming language designed at Google … Go is syntactically similar to C, but with memory safety, garbage collection, structural typing, and CSP-style [communicating sequential processes] concurrency.

Haskell is a general-purpose, statically typed, purely functional programming language with type inference and lazy evaluation.

What’s remarkable about all three of these descriptions is that they are at once highly informative to an experienced reader and utterly baffling to everyone else. By the end of this chapter, you’ll understand every bit of that techno-babble!

Defining a programming language

Programming languages are examples of formal languages: languages defined by a formal specification. They are neat and logical, in comparison with natural languages (e.g. English, Mandarin). Grammar defines the elements of the language and how they can be combined into correct statements. The rules of the grammar are known as the language’s syntax. Knowing these rules, we can write syntactically valid source code and the computer can analyse it to derive the structure of the specified program. We’ll cover this process, compilation, in much more depth in chapter ten.

Syntax is the surface level of how the language looks and feels. Programmers generally like their languages to feel familiar and so certain syntax patterns are common across languages. C uses curly brackets to delimit blocks of code:

1 int function square(int n) {
2   return n * n;
3 }

Both JavaScript and Go have a similar syntax rule. This is what Wikipedia means when it says that JavaScript has “curly-bracket syntax” and Go has “C-like syntax”. This is the same function in Go:

1 func square(n int) int {
2   return n * n;
3 }

There are a couple of minor differences but structurally they look very similar. The same function in Haskell, which is influenced by a different family of programming languages, has completely different syntax:

1 square :: Int -> Int
2 square n = n * n

Syntax only tells us whether a bit of code is a valid fragment of the language. It doesn’t tell us anything about what should happen when that fragment is executed. The behaviour of the language is known as its semantics. The semantics of C, Go and Haskell all specify that we have defined a function called square that takes an integer called n and returns another integer that is the square of n. Even though they are syntactically different, all three functions have identical semantics.

The smallest semantic unit is the expression. An expression is anything that can be evaluated, or computed, to a value. 3 * 3 and square(3) are both expressions that evaluate to 9. Expressions can be composed to create more complex expressions: square(3 * 3).

Many languages have the concept of a statement: an executable chunk of code that might contain expressions but does not itself evaluate to a value. Statements are useful because they produce behaviour known as side effects. For example, an if statement usually has the following structure:

1 if (EXPRESSION) { A } else { B }

The statement controls whether A or B is executed next, depending on whether EXPRESSION evaluates to true or false. Statements such as if, while, for and return control the flow of execution through the program. Other important categories of side effects include mutating program state and input/output. These operations are all useful because of the change in system state they effect, not because they evaluate to a useful value.

If you’re unsure whether something is an expression or a statement, ask yourself whether it is meaningful to assign it to a variable. Generally, assignment only allows expressions to be assigned. This JavaScript example doesn’t work because the if statement doesn’t evaluate to anything status could hold:

1 var status = if (user.isValid) { user.status } else { "no user" }

Origins and communities

Designing a language is fundamentally a creative act. Which syntax rules do you choose and what are the semantics? What are the core concepts underpinning the language and how do they all fit together? There is no single, correct answer to any of these questions and so there is no single, “best” programming language. What is an expression of sublime beauty to one person is a confusing and ugly mess to another. What works wonderfully in one problem space might be hopelessly awkward in another.

The combination of syntax and semantics forms the specification of a language. It defines what is considered syntactically valid code and how that code should behave when executed. The exact format of the specification varies. Commonly, languages start out relying on a single reference implementation. This will be a compiler or interpreter, most likely written by the language’s initial creator(s), that is seen as definitive. The language is defined by how the reference implementation behaves. Later, if the language gains popularity and multiple implementations arise, it might prove useful to write a standardised specification document so that everyone has an agreed understanding of how the implementations should behave.

This is the path Ruby has taken. It began with a reference implementation called Matz’s Ruby Interpreter (MRI) written by Ruby’s creator, Yukihiro “Matz” Matsumoto. It has since evolved into multiple implementations standardised by a formal specification. An interesting thing about Ruby is that the specification itself is written in Ruby as a suite of unit tests. If a program successfully passes all of the tests, then it’s a valid Ruby implementation!

Every language has its origin story. Sometimes the language is written by a lone developer, as Ruby was by Matz and Python was by Guido van Rossum. Sometimes a company might put together a team specifically to create a new language, as Google did with Go. No matter who the creators are, programming languages are made to fix a perceived deficiency. Other languages are too slow, too complex, too simplistic, too lacking in support for this or that idea.

There are many, many programming languages out there and very few of them escape obscurity, let alone become popular. What determines whether a language “makes it”? Sometimes it’s a case of being the right tool for the task. A language’s semantics might make it especially well suited to a particular problem or environment. C originally became popular because it made it easier to write performant code for multiple architectures. Technical merits are not always sufficient. C also enjoyed an association with the killer app of the day: the Unix operating system. Go gained some initial name recognition thanks to its association with Docker and Kubernetes at the start of the container hype cycle.

Technical merits aside, Go undoubtedly owes much of its current popularity to the fact that it is backed by Google and has a paid team of developers working on its core libraries and tooling. Languages without corporate sugar daddies have to rely on their creator successfully building an enthusiastic community of volunteer contributors who will create the necessary ecosystem themselves. The social, community element of programming languages is just as important as it is with natural languages.

The purpose is always to communicate. Writing code is far more than just instructing the computer. That’s the easy part, really. It’s also a communication to all the other developers, current and future, who will read and interact with your code. Using the right language helps us to better express complex, abstract concepts in a way that is readily understandable by both people and machines.

Programming language concepts

In this section, we’ll consider a few questions that will help us understand what distinguishes one programming language from another.

Levels of abstraction

Our first question is: at what level of abstraction does the language operate?

We know from previous chapters that the processor exposes an instruction set architecture (ISA) to software. How closely do the semantics of a programming language match the semantics of the underlying hardware’s ISA? That is, what abstractions does it offer on top of the hardware? If a language offers few abstractions, we say that it is low level. Predictably, a language with a great deal of abstraction is high level. Generally, lower level languages are conceptually simpler and offer more control over the hardware. Higher level languages make it easier to express large-scale applications at the cost of performance and hardware control.

Abstraction refers to concepts that are present in the language but not directly supported by the hardware. For example, a processor will almost certainly have instructions supporting functions (e.g. CALL, RET) but no instructions implementing JavaScript promises. That’s because promises are a high level abstraction that JavaScript creates out of more simple primitives.

To understand a programming language’s abstraction level, a useful exercise is to describe some code in natural language. The nouns you use indicate the abstractions. Imagine we want to describe what an if statement does. An assembly implementation might be expressed in English as follows:

Write this value into that register. Read the value stored in this memory address into that other register. Compare the two values. If the zero flag is set, add this offset to the program counter register. Otherwise, increment the program counter register.

Note that the program deals directly with the system’s hardware elements. It’s actually a little hard to work out the intent. Since each assembly is specific to its ISA, assembly programs are not portable: a program written in one platform’s assembly won’t run on another platform without modification. Assembly doesn’t “abstract away” the details of the underlying ISA.

At one abstraction level higher, C was designed to be a “portable assembly”. Its semantics assume a simple machine model, a little like what we saw in the architecture chapter, which a compiler can easily map to the specifics of the actual hardware. A C implementation could be like so:

If this value equals the value of this pointer, take this branch else take that branch.

Note that it’s much shorter because the precise hardware details aren’t specified. We don’t know in which registers the values are held. We are operating at a higher level of abstraction, though the reference to a “pointer” indicates that one value is held in some memory location. It’s interesting to note that nowadays we think of C as a low level language because its semantics permit using pointers to noodle around the process’ address space. Back in the 1970s, when C was first developed, it was actually seen as a high level language because the code wasn’t tied to any specific ISA.

In a modern, high level language such as JavaScript, Ruby or Python, the same code might be described as:

If this user object’s ID property matches that user object’s ID property, do this else do that.

We’ve lost all the information indicating where the values are physically stored. The language hides such implementation details from us. We are now operating at a level where the hardware is abstracted away and the source code deals directly with the application’s concepts and terminology.

All of the examples ultimately result in the same behaviour but the lower level languages include much more hardware-specific information. Sometimes this is useful (particularly when performance is critical), but often we don’t really care about minor details like which register holds a particular value. Greater abstraction allows high level languages to be more expressive. The same behaviour can be expressed in less code at the cost of less control over the hardware. These considerations are usually in conflict. Very roughly speaking, high level languages optimise for speed of development and low level languages optimise for speed of execution. A small, low level language will offer optimal performance and control over the hardware but the lack of abstraction makes it more challenging and time consuming to write large applications. High level languages make it easier for the developer to express their intent concisely but cannot offer the same level of performance and control. Some languages, such as C++ and Rust, make a brave attempt to have their cake and eat it by providing sophisticated abstractions while still allowing nearly full control over the hardware. These solutions come at the cost of high complexity.

First class values

If programming languages offer varying levels of abstraction, the obvious next question is: what abstractions are available? To answer this, we must look at what first class values the language has. By “first class”, I mean that an instance of the value can be created, stored and passed around just like any other value. Basic types such as numbers and strings are almost always first class, though sometimes with quirks. For instance, JavaScript represents all numbers in 64-bit floating point. Until the introduction of BigInt in 2019, it simply wasn’t possible to create an integer in JavaScript. Writing x = 1 actually assigned the floating point 1.0 to x. We also saw in the concurrency chapter how promises made asynchronous values first class in JavaScript.

If you have ever programmed in JavaScript, you’ll be accustomed to functions as first class values. In JavaScript, functions can be dynamically defined, passed around as arguments, stored in data structures, returned from other functions and so on. Let’s imagine that your application has levels of debugging verbosity and you want to prefix each log output with its debug level. One approach would be to create functions for each debug level:

1 function logger(level) {
2   return function(message) {
3     console.log("[%s]: %s", level, message);
4   }
5 }
6 warn = logger("WARN");
7 error = logger("ERROR");
8 warn("memory running low"); // [WARN]: memory running low
9 error("value out of bounds"); //[ERROR]: value out of bounds

We are doing several magical things in this little bit of code. logger is a function that dynamically creates a new function, using the provided level argument, every time it’s called. The returned function expects a message and logs it with the warning level. JavaScript uses function scope, which means that every variable in logger is visible to the returned function. The combination of a function and its enclosing environment is known as a closure and is a very powerful concept. It enables a function to carry around its own execution environment. In the example above, two logging functions are generated and assigned to warn and error, each with a different value for level in their execution context.

If, like me, you began programming by learning JavaScript, all of this might seen very unremarkable. Yet it’s surprisingly hard to do in many languages. In C, you can’t easily dynamically generate functions or pass them as arguments to functions. All you can do is pass around a pointer to the function. It is not possible to write a function that creates and returns a new function as we do in logger above. Even Ruby, focused as it is on increasing developer joy, makes this tricky. In Ruby, referring to a function is the same as calling it, so passing around a function without calling it requires wrapping it in an executable object known as a Proc:

1 def logger(level)
2   Proc.new{ |msg|  print "[#{level}]: #{msg}" }
3 end
4 
5 warning = logger("WARN")
6 warning.call("I've got a bad feeling") # [WARN]: I've got a bad feeling

Note that logger, which is a function, is called differently to warning, which is a Proc. That distinguishes the Proc from a true function.

State management

Most languages have the concept of a variable: a named memory location that holds a value. The program’s state is the collection of all its variables’ values and the current execution point. This brings us to our next question: what mechanisms does the language provide for managing state?

Continuing with JavaScript examples, here we declare a variable called user and assign to it an object:

1 let user = { firstName: "Tom", surname: "Johnson", isAdmin: false };

We have associated the identifier user with the object. The memory location assigned to user holds the bytes of the object. We can query the object to determine its state. For now, user.isAdmin returns false. So far, so simple. Yet as the word “variable” implies, user can vary. When we modify the variable, things get complicated:

1 let user = { firstName: "Tom", surname: "Johnson", isAdmin: false };
2 user.isAdmin = true;

Now the same identifier is associated with two different objects at two different points in time: one in which isAdmin is false and one in which it is true. The question “is the user an admin?” becomes difficult to answer because the answer depends on when we ask it. When state can vary, we say that it is mutable. To reason correctly about mutable state, we need to include time in our model. The value of a variable may change between two time points. Mutable state aligns with how the underlying hardware works (you can write to a memory cell as much as you like) and so most programming languages allow mutable state. The disadvantage of mutable state is that it can lead to confusing bugs, particularly if the state is shared between multiple threads (see the concurrency chapter).

Immutability

One way to avoid shared, mutable state is to prefer immutability. In languages with immutable state, it is not possible to change the value associated with a particular identifier. To perform a modification, you need to create a new value with the desired changes. JavaScript is by default mutable and offers opt-in immutability with the const keyword:

1 const name = "Tom";
2 name = "Timmy"; // TypeError: invalid assignment to const `name'

The problem with opt-in immutability is that it’s easy to forget. Then you lose the guarantee that a variable will maintain the expected value. Immutability by default is a more extreme approach that’s pretty popular in functional programming languages (discussed in more detail below). To them, mutable state is an abomination that should be expunged or, at the very least, used as little as possible.

What we have here are different answers to the old philosophical problem. How does a river remain the same “thing” when its contents and shape are constantly changing? In a language with mutable state, the value associated with an identifier can change. There is only one river but it varies over time. In languages with immutable state, the identifier’s value can’t be modified. Each change results in a new object.

Clojure is particularly interesting in this regard because it is inspired by Alan Whitehead’s process philosophy. Clojure is a functional, immutable-by-default language. Immutability entails a performance cost because it is more expensive to create an entirely new variable than to modify an existing one. Imagine you had an array of one million elements and wanted to append a new one. It would be madness to fully duplicate the entire array just to add one element. To avoid this, Clojure uses “persistent” data structures. Modifications are recorded as incremental changes against the previous version, similar to how version control systems record a series of diffs against an original. Persistent data structures record a single entity with different values at different points in time. In this world view, our river is actually a sequence of different rivers that we can access by sliding time back and forth.

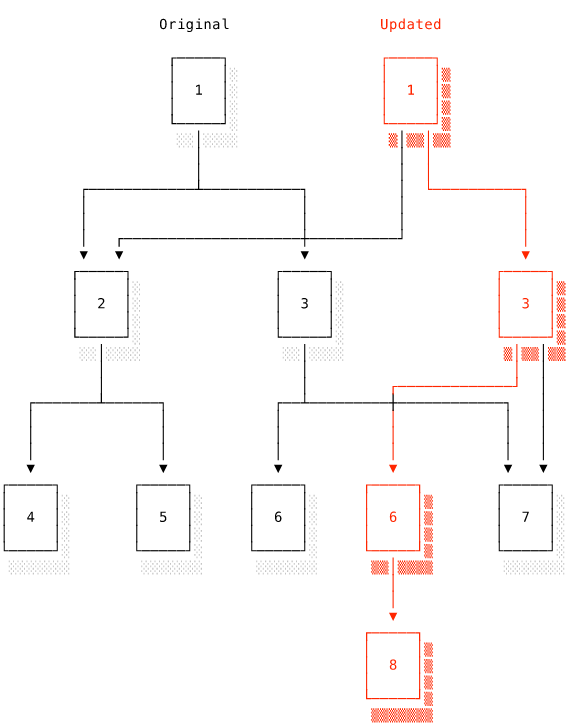
Here we have a tree modified to hold an extra element. The original tree on the left has seven nodes. Each node holds a value and pointer(s) to children. When we modify the tree by adding a new value, the parent node needs to be updated to hold the new pointer. We must create a new version of the parent with a pointer to the new node. Since the parent has been updated, we must update its parent and so on recursively up the tree until we hit the root. The red nodes in the diagram are the new versions. Where the nodes have not been modified, the new tree can reuse the old nodes. Note that the updated tree still makes use of the whole sub-tree with root 2. By making only the minimum necessary changes, the persistent data structure offers efficient immutability.

Objects

A second solution to shared, mutable state is to keep the mutability but avoid sharing as much as possible. We greatly reduce the occurrence of confusing bugs if we can hide mutable state away and reduce the amount of code that can directly interact with it. The combination of state and associated behaviour is known as an object. Objects hold their state (mutable or immutable) in private variables known as fields. Only procedures belonging to the object, known as methods, are allowed to directly interact with the fields. The object can choose which fields and methods to make accessible to the outside world. The rest of the codebase can only interact with the object through this public interface:

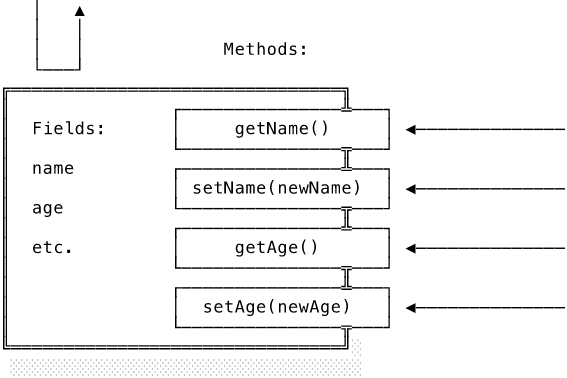
The object presents an impermeable barrier to the outside world. The methods on the right straddle the barrier. The only way to access the object’s state is through the interface the object chooses to offer via its methods. At the top left, we see a rebuffed attempt to bypass the methods’ interface. Instead of having state open to arbitrary mutation, the object controls how its internal state can be accessed and modified. I’ll have much more to say about objects when we look at object-oriented programming below.

Memory management

We finish up with a related question: how does the language manage programs’ memory usage? In all but the most trivial programs, it will be necessary to allocate memory at runtime. A web server, for example, will need to allocate memory for each request it receives. The programmer cannot possibly know how much space to allocate in advance, so it must be done while the program is running. Once the memory is no longer needed (perhaps because the server has finished handling the request), it must be returned to the pool of available memory. Otherwise, the program will gradually allocate more and more memory until the system runs out of memory.

Memory management is a distinguishing characteristic of programming languages. At one extreme we have (again) C, where the programmer is responsible for manually managing the dynamic allocation of heap memory (refer to chapter three if you’ve forgotten that term). The C standard library provides a couple of helper functions to request memory blocks and release them when no longer needed (malloc and free, respectively). Other than that, you’re on your own. “Call malloc when you need memory and free when you’re done” sounds straightforward but it’s very easy to get wrong, especially in a large program. For this reason, many languages implement some kind of automatic memory management. When you declare a variable in Go, for example, the compiler decides whether to store it on the stack or the heap, allocating and freeing memory as required.

Automatic memory management often uses garbage collection. The language runtime keeps track of which resources are still in use and marks unused ones as “garbage” to be collected and returned to the heap. A simple technique is reference counting, in which the runtime tracks how many references there are to each resource. Once there are no more references to a resource, it is marked as garbage. Another commonly used algorithm is mark and sweep. Starting from one or more root resources, the garbage collector follows every reference to other resources, marking each one as reachable as it goes. Once it has marked every reachable resource, any remaining resources are unreachable and can be swept away.

Commonly, the language runtime will periodically pause normal execution to perform garbage collection. This obviously implies a performance cost. Worse still, the occurrence of these “stop the world” pauses is non-deterministic and not something the program can predict or manage. For these reasons, languages with automatic memory management are rarely used when predictable performance is essential (e.g. operating systems). Rust is a relatively new language that uses its type system to provide a form of compile-time memory management with zero runtime cost.

Programming paradigms

The questions we’ve considered help us to determine the programming paradigms a language supports. In broad terms, a paradigm represents a world view, a particular set of concepts with which the programmer can express their intent. It’s common for a language to focus primarily on one paradigm, though some attempt to be genuinely multi-paradigm.

Imperative programming

In the imperative programming model, the program is an ordered sequence of statements. The programmer writes instructions to explicitly control execution flow. Each statement may evaluate expressions and perform side effects, such as modifying a variable in memory. Imperative code is so called because it instructs the computer how it should generate the desired result. Imagine the programmer as an all-powerful Roman emperor sending out detailed commands. At its core, imperative programming is conceptually quite simple because it maps closely to how the hardware executes the underlying machine code. Assembly languages are good examples of simple imperative languages. Most mainstream programming languages are imperative at heart.

Procedural programming

The first innovation within imperative programming was the invention of the procedure, also known as the function or subroutine. Procedures allow related instructions to be encapsulated into reusable chunks. They provide modularity because everything that the procedure does occurs within the procedure’s scope, which is not visible from outside of the procedure. Scoping and procedures thus help to compartmentalise code into logical units with minimal data sharing. Code that calls a procedure doesn’t need to know anything about how the procedure functions internally. It only needs to know the procedure’s interface: the arguments it accepts and its return value. Overall, procedures mean that less state is globally accessible and help the programmer to structure their program as blocks of reusable functionality.

Procedural languages arose around the end of the 1950s / early 1960s with languages such as FORTRAN and COBOL. Although they are both still used, by far the most popular procedural language is C (1972). As I mentioned above, C was designed to be close to the hardware but easily portable across systems. The combination of portability, speed and hardware control makes it still hugely popular for “systems” programming tasks, which include operating systems, compilers, servers and so on. C is also closely associated with the Unix operating system and its descendants. The Linux kernel is written in C.

A simple but complete C program looks like this:

 1 #include <stdio.h>
 2 
 3 int find_max(int arr[], int count) {
 4   int i, max;
 5 
 6   max = arr[0];
 7 
 8   for (i = 1; i < count; i++) {
 9     if (arr[i] > max) {
10       max = arr[i];
11     }
12   }
13 
14   return max;
15 }
16 
17 int main() {
18   int arr[] = {2, 84, 32, 11, -70, 199};
19   int n = sizeof(arr) / sizeof(arr[0]);
20 
21   printf("Largest element is %d\n", find_max(arr, n));
22 
23   return 0;
24 }
25 // Prints: Largest element is 199

Without going through the code line-by-line, I’d like you to note that the “find the max element in this array” functionality is abstracted away into into the find_max function. The function’s definition tells us that it takes an int array and an int as arguments and returns another int. The variables i and max are local to the function and so are not visible outside of the function. They exist in the function’s stack frame, which will be destroyed when the function returns. The value of max will be copied and returned. It would be easy to change the implementation of find_max without having to change any other code, so long as it still fulfilled the interface.

You might be wondering why we calculate n (the number of elements) and pass it to find_max. That’s because arrays are not really first class values in C. When we pass arr to find_max, all that actually happens is that find_max receives a pointer to the first element in the array. The array doesn’t record its own length and so with just a pointer to the first element, we don’t know how long the array is. We need to work out the length as the byte size of the array divided by the byte size of a single element and then pass it around in a separate variable. Modifying the array without updating the size variable, and vice versa, is a common source of bugs in C. That’s why later languages generally offer the “smart” arrays we saw in the data structures chapter as first class values. Note too that the state, the array, and the operation on the state, find_max, are conceptually and physically separate.

Object-oriented programming

Object-oriented programming (OOP) develops the ideas of modularity and encapsulation a step further by moving state into objects. As described previously, an object is a bundle of private state coupled with methods that operate on that state. Objects were first popularised by Alan Kay in the Smalltalk language (1970s) but really had their heyday in the 1990s (along with Nirvana and anti-globalisation protests). That era saw the rise of C++, Java and then later Ruby and Python. All are object-oriented. Nowadays, the majority of languages in widespread use include at least some support for OOP.

Most object-oriented languages use classes to define objects. A class is a template for generating objects of a particular type. Think of how a cookie cutter stamps out cookies of an identical shape. A constructor function creates objects that are instances of the class. Classes are used to model the entities in a program. Their fields hold their private state and their methods define how they interact with each other. Methods are special functions with an extra argument, normally called self or this, that provides access to the object’s private properties. Usually, the extra argument is implicit although Python explicitly requires it: def my_method(self, my_arg). By only allowing access to its private state via this extra argument, the object ensures that only its own methods have unrestricted access to its state. This is known as encapsulation. Here’s an example using a simplified Java:

 1 public class User {
 2   private LocalDate dateOfBirth;
 3 
 4   // Constructor
 5   public User(LocalDate dateOfBirth) {
 6     this.dateOfBirth = dateOfBirth;
 7   }
 8 
 9   public boolean canDrink() {
10     LocalDate today = LocalDate.now();
11     Period age = Period.between(this.dateOfBirth, today);
12     return age.getYears() >= 18;
13   }
14 }
15 
16 User user = new User(LocalDate.of(2010, Month.MAY, 20));
17 user.canDrink() // false
18 user.dateOfBirth = LocalDate.of(1990, Month.MAY, 20); // ERROR

This Java class declares its dateOfBirth property to be private so that it cannot be accessed from outside of the class. The canDrink method uses the private state to compute whether the user is of legal drinking age. There is no way for code elsewhere in the program to circumvent this restriction by modifying the date of birth. The class has thus enforced its desired behaviour.

Object-oriented programming is not just about managing mutable state. Its proponents argue that it also helps to make software more modular and more easily extensible. At first glance, it doesn’t really seem to make much difference whether you stringify a variable by calling a method variable.toString() or by calling a function toString(variable). Think what would happen, though, if we added a new data type and wanted to be able to stringify it. If we used a single toString() function, we’d need to modify toString()’s implementation to support that new data type. Adding a new data type therefore requires changes to other parts of the codebase to support the new data type. In object-oriented programming, we would define a new class for the data type and implement all of its functionality there. The rest of the codebase does not need to change to support the new data type. It can just call the .toString() method and rely on the object to provide a suitable implementation. This is known as polymorphism and is a central concept in object-oriented design.

In its purest form, object-oriented programming is more than just “programming with objects”. An analogy with biological cells is useful. Imagine an object as a cell that has engulfed some tasty data molecules. The cell membrane acts as an interface between those data molecules and the outside world, controlling what may enter and leave the cell interior. It is not possible to access the cell’s internal molecules without going through the membrane interface. Similarly, an object’s fields are only accessible from within the object’s scope. We can’t pry into the object’s internal structure or state. We can only observe how it chooses to respond to messages. Cells communicate by releasing chemical messages. Objects pass messages by calling methods. When you see a method call like name.toString(), think of it as passing the message (or command) “give me a string representation of yourself” to name. It’s up to name to decide whether and how it wants to respond.

Each object is a self-contained mini-computer focused on a single responsibility. Complex programs can be broken down into lots of simpler mini-computers that only communicate through their method interfaces. Computation becomes more organic, occurring in lots of objects simultaneously. The biological analogy breaks down in reality, however. Real cells emit chemical messages without any knowledge of what other cells are in their vicinity to receive the messages. In order to send a message to an object, you need to have a reference to it so that you can call its method. In object-oriented programs, managing references to objects can become a complex design issue. Often programs end up using some kind of central holding object, very unlike the decentralised biological analogy.

Critics argue that object-oriented programming thus fails to deliver on its promises. Proponents counter that, just like communism, the idea is fine but it has never been implemented properly in reality. Popular object-oriented languages don’t do it right and that’s why things don’t always work out. While perhaps true, this does make you wonder why object-oriented programming is so hard to implement properly in the first place. The best example of actually existing, object-oriented design is, surprisingly, the Internet. Servers are objects with private, internal state that only communicate via public interfaces. Servers broadcast messages with only limited knowledge of which neighbouring servers will receive and process their messages.

When you write object-oriented code, it’s easy to fall into the trap of thinking that objects are somehow special. Looking at the Java example above, we have that special class keyword and special handling of methods so that this is implicitly available. Pretty much all Java code has to live within a class. But don’t let the syntax mislead you. Here’s the Java class above recreated in JavaScript using functions and closures:

 1 function User(dateOfBirth) {
 2   let _dateOfBirth = dateOfBirth;
 3 
 4   function canDrink() {
 5     let today = moment.now();
 6     return _dateOfBirth.diff(today, "years") >= 18;
 7   }
 8 
 9   return {
10     canDrink: canDrink
11   }
12 }
13 
14 let user = User(moment("2010-5-20"));
15 user.canDrink(); // false
16 user._dateOfBirth = moment("1990-5-20"); // ERROR

_dateOfBirth is declared within the scope of User and so it is not accessible from outside of User. It is hidden, just like a private class field would be. User defines canDrink, which has access to _dateOfBirth, and makes it publicly accessible by returning it in an object. The user variable holds the returned object, so consuming code can call user.canDrink() like a method. It’s interesting to see that objects and closures, though on the surface appearing to be very different, are actually very similar on a deeper, semantic level.

Declarative programming

Recall that an imperative program is an ordered sequence of statements. In the declarative programming paradigm, the programmer declares the results they want and lets the computer figure out how to compute it. Imperative programming says how to generate the result, declarative programming says what the result should be.

Declarative languages tend to avoid explicit control flow. After all, we’re not telling the computer what to do. As we’re only describing the desired result of the computation, declarative languages also tend to avoid side effects such as mutating state. A consequence of this is that they often prefer to use recursion, a function calling itself, instead of loops and mutable counters.

Don’t worry if declarative programming sounds a little esoteric. Most people learn programming in an imperative style and other approaches initially feel odd. In fact, you’ve already seen one declarative language: SQL. When we write a SQL query, we define the shape of the desired result and the database engine’s query planner goes away and works out how to compute it. That’s exactly how a declarative language works. Regular expressions are another example of declarative languages. An interesting branch of declarative programming is known as logic programming, in which programs are expressed as a series of logical statements and the computer tries to find a solution to the statements. Due to space constraints, I can’t go into more depth here but I encourage you to check out Prolog.

A more common branch of declarative programming is functional programming. In this paradigm, a program consists of function application and composition. In other words, lots of functions calling lots of other functions. Haskell is a popular example of a functional programming language. A simple Haskell example serves to show the key concepts of declarative programming:

1 length [] = 0                 -- empty list
2 length (x:xs) = 1 + length xs -- non-empty list

length calculates the length of a list. We provide two definitions. The first is for an empty list, which obviously will have a length of zero. In the second definition, we use (x:xs) to split the list into the head x and the tail xs. The length will be equal to the length of the tail plus one. The function calls itself recursively, each time producing a one and a shortened list, until it hits the base case of an empty list, at which point the recursion stops with a zero. The result is the sum of all of the ones. Note that there is no control flow. There is no code that checks whether the list is empty. We just declare what should happen in both cases and leave the computer to decide what to do.

The key feature of functional programming is that functions are first class values. This makes it possible to write a program as a composition of functions. Even non-functional languages can offer support for a functional “style” if they provide first class functions. As an example, JavaScript supports a functional style of programming by allowing functions to be passed to other functions:

1 [1, 2, 3].map(x => x * x); // [1, 4, 9]

Note that in this style we don’t have to maintain a counter and iterate through the array. The map implementation handles all of that, only requiring us to plug in the function we want to execute at each step.

The more hardcore form of functional programming requires that functions are pure, meaning that they have no side effects. A pure function will always give the same output for a given input. x => x * x will always return 9 when passed 3. This makes the functional expression easier to reason about because it can always be substituted for the value it evaluates to. Haskell is famous for requiring that functions are pure. Of course, reading user input, writing to the screen and other side effects are very useful. Haskell has to provide notoriously confusing mechanisms to contain impure behaviour within pure functions.

Popular functional languages include Haskell, Clojure and Ocaml. Not all of them demand pure functions in the way Haskell does but they do tend to minimise mutable state as far as possible. Proponents of functional programming see it as cleaner and more elegant, closer to a mathematical ideal, than imperative programming, which is hopelessly mired in the reality of mutable state. In recent years, functional programming has become increasingly popular as people find that minimising mutable state makes their programs easier to write, debug and reason about. A lack of shared, mutable state also makes concurrent programming much easier to do in functional languages.

Type systems

A data type defines a “shape” data can have. It defines the set of possible values and the operations that can be performed on those values. For example, the boolean type can be either true or false and it supports logical operations such as negation, conjunction and disjunction. The string type is the (infinite) set of character sequences and it supports operations like concatenation and substitution. A type system defines and enforces a set of type rules specifying how types are assigned to expressions and how types interact. Some types are built in to the language and normally there is some mechanism for user-defined types.

Type theory, the academic study of type systems, is one of those areas where computer science meets mathematics. In fact, there is a proven equivalence between computer programs and logical proofs. We’ll look at the implications of this shortly, but for now look at the following type rule: A -> B. As a logical proof, this means “A implies B”. As an expression in a typed programming language, it’s a function that takes type A and returns type B. A concrete example would be length :: string -> int. It takes a string and returns an integer. Types provide a more logically robust way to think about computer programs and their correctness.

Types are a powerful tool to express intent both to the computer and to other people. Type systems improve correctness by making explicit how parts of the system should interact with each other. That gives the computer more information with which it can detect errors. Type checking is the process of verifying that all of the constraints imposed by the type rules are met by the code. If the computer knows that length only accepts strings, it can catch bugs where we mistakenly pass a different type to length. The more type errors that a type system can detect, the more type safe it is. Some argue that by creating ever more sophisticated type systems, we can encode more and more information in the type system and thus gain more and more type safety. Others argue that complex type systems add unnecessary complication and get in the way of expressing application logic.

Every language has a type system, even if it’s not very obvious or helpful. Type systems are categorised along two main axes: static versus dynamic type checking and strong versus weak typing. In this diagram, languages are categorised into quadrants by their type system:

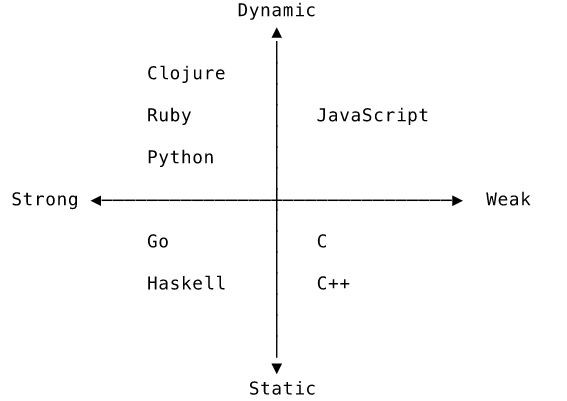
Static and dynamic type checking

Type checking is the process of validating that every expression has a valid type according to the rules of the language’s type system. If the program passes, it is type safe. Static type checking happens before the program runs and dynamic type checking happens while the program is running.

A statically typed language verifies that a program is type safe by analysing the source code before the program even runs, normally as part of the compilation process. An obvious implication is that the source code needs to contain enough information for the type checker to work out the types without having to run the code. This might be done by annotating a variable with its type in the source code. In Go, the type comes after the variable name:

1 var message string = "I'm a string!"

This is redundant though, right? It’s obvious that the value is a string literal, so we shouldn’t really need to specify it. The process of automatically determining the type of an expression is known as type inference. A type system with inference doesn’t require so many manual annotations because the type checker can determine the type of many expressions from context. Go supports type inference using what is known as “short declaration syntax”:

1 message := "I'm a message!"

Static type checking provides assurance that the types of expressions match our expectations. A function’s type signature documents what it accepts and what it returns. In the following example, welcomeShout defines its argument to be a string. The last line contains a type error and so the program will not even compile:

 1 import (
 2         "fmt"
 3         "strings"
 4 )
 5 
 6 func welcomeShout(name string) {
 7         fmt.Printf("Welcome, %s!\n", Strings.ToUpper(name))
 8 }
 9 
10 func main() {
11         welcomeShout("Tom") // Welcome, TOM!
12         welcomeShout(42) // Compiler error
13 }

In a dynamically typed language, type safety is only verified at runtime. A common implementation is that each variable has a type tag containing type information. When an expression is evaluated, the runtime first checks that the operands’ types are compatible with the type system’s rules. The problem with dynamic typing is that we can’t check in advance whether the operands’ types are correct. We can only run the code and see if it works:

1 function welcomeShout(name) {
2     console.log(`Welcome, ${name.toUpperCase()}!`);
3 }

In this equivalent JavaScript code, the function implicitly expects name to be a string (or another type that responds to toUpperCase), but it has no guarantee that the argument is the correct type. If name doesn’t respond to toUpperCase, the code will throw a runtime exception and probably break the program. Applications in dynamically typed languages require extensive test suites to try and cover every code path. Even with a huge test suite, it is impossible to be completely confident that every broken code path has been found. In a statically typed language, by contrast, the compiler will detect the broken code paths caused by type errors and will refuse to run the program until they are fixed. That can be frustrating when you just want to run a small section of the code or try out an idea and you know that the type errors aren’t immediately problematic. The advantage is that once it finally does run, you can be more confident that the code will work.

The main benefit of dynamic typing is that it is easier to get started and try out ideas without the up front work of codifying lots of rules in the type system. It lends itself to a very flexible and permissive style of programming. For example, a log processor might iterate through a stream of logs. In Ruby:

1 class Parser
2   def parse(input)
3     input.each do |line|
4       # ...processing here
5     end
6   end
7 end

We can pass absolutely anything to #parse, as long as it implements the #each method. In production, this might be some kind of sophisticated event stream. In testing, we could just use a simple array because Ruby arrays implement #each. We don’t need to define in advance what types #parse is allowed to receive. Python programmers like to call this “duck typing” with the slightly grating explanation that “if it walks like a duck and quacks like a duck, it’s a duck”. We don’t really care about the actual type of input. We only care that it implements each.

Interfaces are a way to bring the flexibility of duck typing into a statically typed language. An interface defines a specification, normally as a set of method or function signatures, that a type must implement to be considered an instance of the interface. By using interfaces, we only specify the behaviour we expect from a type. Structural typing is when a type automatically implements any matching interface. Go and TypeScript (a typed superset of JavaScript) both take this approach. Nominal typing requires a type to explicitly declare the interfaces it implements. It isn’t enough to just fulfil the interface’s specification. Neither approach is better or worse. Structural typing allows for a statically checked version of duck typing while nominal typing better conveys intent.

In Go, the standard library’s Stringer interface is for types that offer a string representation of themselves. We could rewrite welcomeShout to accept a much wider set of types by changing it to expect an interface:

 1 import (
 2         "fmt"
 3         "strings"
 4 )
 5 
 6 type Stringer interface {
 7     String() string
 8 }
 9 
10 type User struct {
11     name string
12     id uint
13 }
14 
15 func (u User) String() string {
16     return fmt.Sprintf("%d: %s", u.id, u.name)
17 }
18 
19 func welcomePrint(name Stringer) {
20         fmt.Printf("Welcome, %s!\n", strings.ToUpper(name.String()))
21 }
22 
23 func main() {
24         welcomePrint(User{id: 42, name: "Tom"})
25 }
26 // Welcome, 42: TOM!

Here I’ve redefined Stringer to show you what an interface’s definition looks like. We define a new type, User, that has a String() method and so implements the Stringer interface. welcomePrint is amended to accept an argument of type Stringer. We have the (statically checked) assurance that any type passed to welcomePrint will provide the necessary String() method and the freedom to pass in any suitable type of our choosing.

In languages with interfaces, it’s good practice to type function arguments as interfaces, rather than concrete types. That gives the function user the freedom to choose the most suitable concrete type for their use case. Interfaces allow us to define new functionality at the type level. For example, Stringer creates the concept of “something that has a string representation”. Using interfaces allows functions to define the functionality they require without unduly constraining their callers.

To recap, in a static type system, type checking is performed before the program runs, using some combination of manual type annotation and automatic type inference. It catches many bugs before the program even runs and helps to document intent. Dynamic typing defers type checking until runtime. That makes it easier to quickly write flexible, reusable code but creates many opportunities for runtime bugs.

Strong and weak type safety

The second axis of type systems reflects how much type safety the system provides. A stronger type system will have stricter type rules and catch more errors, presenting them as compilation errors or runtime exceptions depending on when the type checking happens. A weaker type system will permit more ill-typed expressions and contain more “loopholes” that allow the programmer to subvert the type system. Obviously that means it will catch fewer mistakes. It may even implicitly convert an invalid type into a valid one in an attempt to avoid type errors. “Strong” and “weak” are not very precisely defined terms. Type safety is more of a spectrum than a binary definition.

C is a weakly typed language with static checking. Variables are typed, but types in C serve mostly to indicate how much space the compiler should allocate for the value. C has weak type safety because we can tell C to reinterpret a variable’s bit pattern as a different type by taking a pointer to the variable and typecasting it to a pointer to the new type. Imagine that you are studying floating point numbers and want to examine the bit arrangement of a floating point number. You can do this by typecasting a pointer to the variable to a pointer to a byte:

 1 #include "stdio.h"
 2 
 3 int main() {
 4   double value = 0.63;
 5   unsigned char *p = (unsigned char *)&value;
 6 
 7   for (int i = 0; i < sizeof(double); i++) {
 8       printf("%x ", p[i]);
 9   }
10 }
11 // Output: 29 5c 8f c2 f5 28 e4 3f

double is C’s name for a floating point number (normally eight bytes wide) and unsigned char is a byte value. The syntax is a little funky but on line five, reading from the right, we use & to make a pointer to value and then cast it using (unsigned char *) from a double pointer to an unsigned char pointer. If we take the hexadecimal output and interpret it as a floating point number, we get 0.63: back to where we started. At no point does the underlying sequence of bits in value change. We only instruct the computer to interpret those bits as two different types, thus generating two different outputs.

Typecasting is usually avoided because it weakens the assurances type checking provides but it can be helpful when working very close to the hardware. Much of C’s design is based on the principle that the programmer knows what they are doing and shouldn’t be impeded by the language. That’s why it allows the use of pointers to arbitrarily manipulate memory and typecasting as an escape hatch in its type system. C’s type system will statically check the types you specify but allows you to deliberately step outside the type system’s protection when you deem it necessary.

JavaScript’s type system is widely considered to be an unholy mess because it combines weak typing with dynamic checking. Not only are types not checked until runtime, but, in an attempt to avoid type errors, JavaScript will silently change, or coerce, an ill-typed value into the expected type, almost certainly resulting in unexpected output. It’s not so much a type system with an escape hatch as a giant sieve. Due to the silent coercion, type errors propagate unseen, eventually popping up in the form of bizarre bugs far from the original error site.

Yet even in this madness there is reason. Remember that JavaScript’s original purpose was to add a bit of sparkle to static websites. JavaScript content was expected to be very much secondary to the rest of the page’s content. JavaScript therefore tries to be resilient so that a JavaScript bug doesn’t stop the whole page from rendering. In that context, when faced with a mis-typed operation such as 1 + "2", it is better to coerce one operand to the expected type and carry on. In this case, JavaScript cannot add a string to a number so it implicitly converts the number to its string representation. Implicit coercion allows JavaScript to produce something vaguely useful instead of just throwing a runtime exception and crashing the page. Admittedly, 1 + "2" = "12" might not be what you intended. I like to think of JavaScript as a really, really keen puppy that just wants to play even when it doesn’t really know how to:

 1 > 4 + 4 // Add two numbers? Sure!!!
 2 8
 3 > "hello " + "there" // Add strings? I'll concatenate them!! Yes!
 4 "hello there"
 5 > "hello " + 5 // Add a string and a number? Hmm... wait I know!!!!
 6 "hello 5"
 7 > "" + {} // You must want the object as a string!! Look!!!!
 8 "[object Object]"
 9 > {} + "" // No problem!!!!!
10 0

Okay, it gets carried away sometimes. Clearly, JavaScript’s weak typing rules can lead to some weird outputs. If those weird outputs happen to be valid inputs for another function, you won’t notice the error until another part of the codebase starts producing even weirder output.

Ruby’s type system is stronger than JavaScript’s because its rules don’t allow sneaky workarounds like implicit coercion. Its type rules catch more errors and have fewer escape hatches. If you try something ill-typed, the interpreter will point out that you’re trying to do some damn fool thing and refuse to proceed:

1 > 1 + "2"
2 # TypeError (String can't be coerced into Integer)

Haskell is the poster child for strong typing because it has a sophisticated type system that allows more of an application’s rules and behaviour to be encoded as types. As a simple example, many languages have a null type to represent the absence of a value. In some weaker type systems, a typed value can also be null, leading to type errors if the programmer forgets to check for null. Java is notorious for this because it allows any reference to an object to be null. Haskell provides a type, known as Maybe, that encodes a possibly null value. Here is an example using numbers:

1 data Maybe Number = Just Number | Nothing

Just is a kind of “wrapper” type around the number. Nothing is Haskell’s way of representing null. I have slightly simplified this code to avoid getting caught up in unnecessary complexities in how Haskell handles numbers.

Let’s see how we might use this type to catch bugs. In floating point calculations, the value NaN (not-a-number) represents undefined or unrepresentable values. Haskell returns NaN when you try to take the square root of a negative number, since that’s an invalid operation. Any arithmetic with NaN generates more NaN values: NaN + 2 = NaN. Awkwardly, NaN is still a numeric type, even if it’s not a valid value, so a function expecting a number will accept NaN. It’s super easy to forget to check for NaN and produce invalid calculations. We can write a safe version of sqrt that return a Maybe Number:

1 safeSqrt :: Number -> Maybe Number
2 safeSqrt n | n >= 0 = Just $ sqrt n
3            | otherwise = Nothing

We declaratively define two implementations for safeSqrt and let the computer select the correct one based on whether n >= 0. If the input is valid, we compute the square root and wrap it in a Just. Otherwise, we return an empty Nothing. The joy of Maybe is that the Haskell compiler will error if we don’t handle both possibilities like so:

1 printOutput n = case safeSqrt n of
2   Just x -> putStrLn $ "sqrt of " ++ show n ++ " is " ++ show x
3   Nothing -> putStrLn $ "invalid input " ++ show n

In Haskell circles there is a popular refrain to “make illegal states unrepresentable”. The aim is to encode the business logic of the application into the type system so that code expressing incorrect business logic would generate a type error and fail to compile.

That approach builds on an important theoretical result in computer science known as the Curry-Howard isomorphism. It states that type systems are equivalent to mathematical proofs. A type corresponds to a logical proposition and if you can provide an instance of the type then you have proved that the type is inhabited and the proposition is true. What the Curry-Howard isomorphism tells us is that in writing correctly typed programs we are proving theorems about the behaviour of our programs. In theory, we could prove any behaviour that could be encoded as a proof. In practice, we are limited by the expressiveness and power of our languages’ type systems. An active area of programming language research is to create much more logically sophisticated type systems so that more complex behaviour can be defined and enforced by the type system.

Conclusion

Programming languages are defined by a specification consisting of the language’s syntax and semantics. The format of a specification might range from an informally defined reference implementation right up to an international standards committee. Syntax defines what is considered valid code. Semantics define how valid code should behave.

Languages are distinguished by the abstractions they offer the programmer over the basic hardware primitives. Low level languages provide more control over the hardware but offer fewer tools for building complex applications. High level languages focus on developer productivity, portability and expressiveness at the cost of hardware control and speed. How languages control state and memory management influence the abstractions they offer.

Imperative programming languages see programs as a sequence of computational instructions. Declarative programming languages see programs as a specification of the desired computational output. Both paradigms are well represented by modern programming languages, especially by object-oriented programming and function programming respectively.

Type systems are a mechanism for defining and enforcing semantics. Type checking is the process of ensuring that a computer program behaves in accordance with the type system. This can either be performed statically, before the program is executed, or dynamically at runtime. Type systems vary in how strongly their rules restrict the behaviour of programs. Strong, static type systems are favoured when improved runtime correctness is important. Dynamic type checking and weak type systems can be useful when flexibility and ease of development are more important.